どうも、かきのたねです。
昨日はセンター試験でしたね。今回は2019年度のセンター物理をわかりやすく解説していきます。
次は第4問。





問1:非慣性系と慣性力 答:3
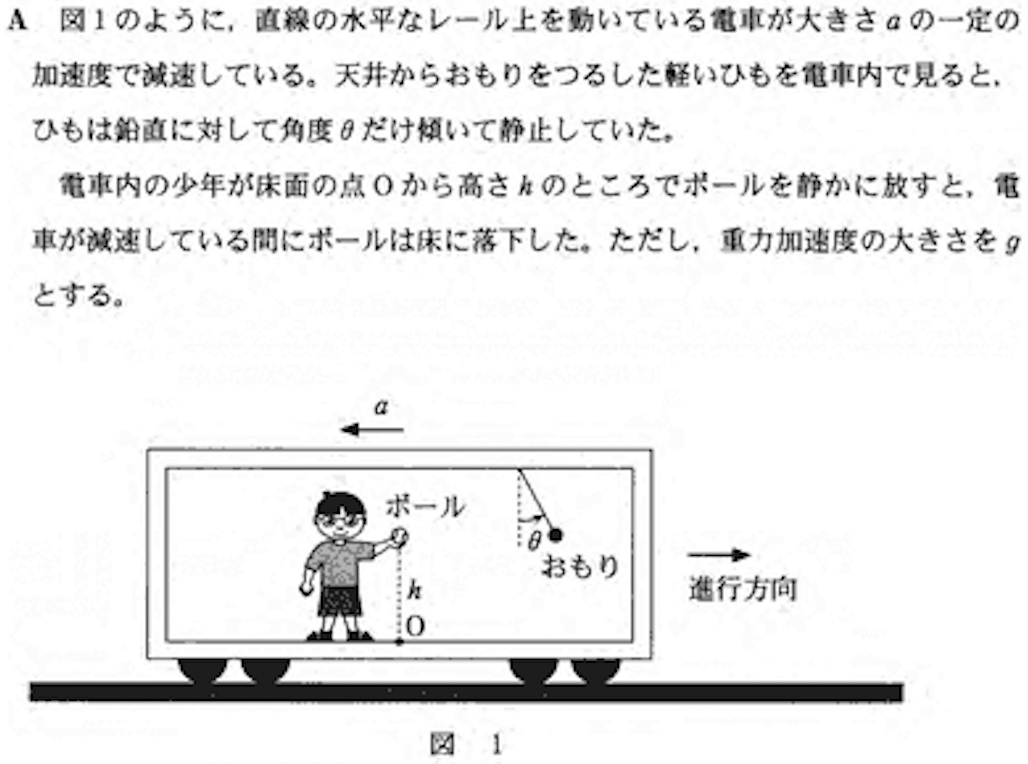
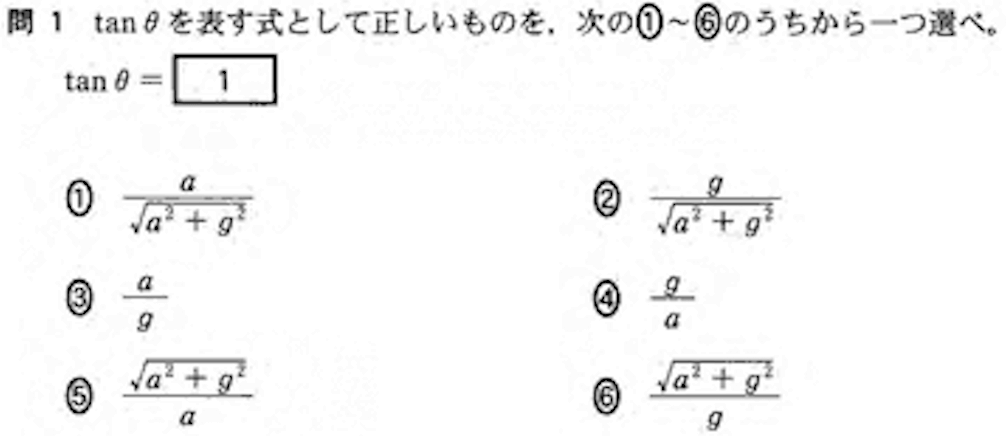
【公式】非慣性系
加速度\( a \)で運動する観測者には、全ての物体(質量\( m \))が加速度の向きとは逆向きに重力のような力(慣性力)\( ma \)が働いているように見える。
エレベーターやバスなどは加速度運動するが、慣性力の大きささえわかれば外界がどう見えるか(自分がどんな速度で運動しているのか)は無視できる。
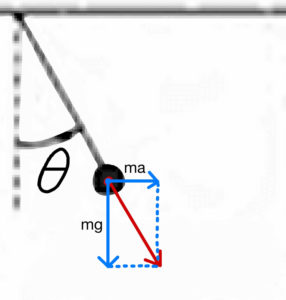
バスの中からこの物体を見ると、重力と張力と慣性力が釣り合っている。
重力と慣性力の合力は赤い矢印で、この図から、
よって3が答え。
問2:非慣性系での物体の運動 答:5
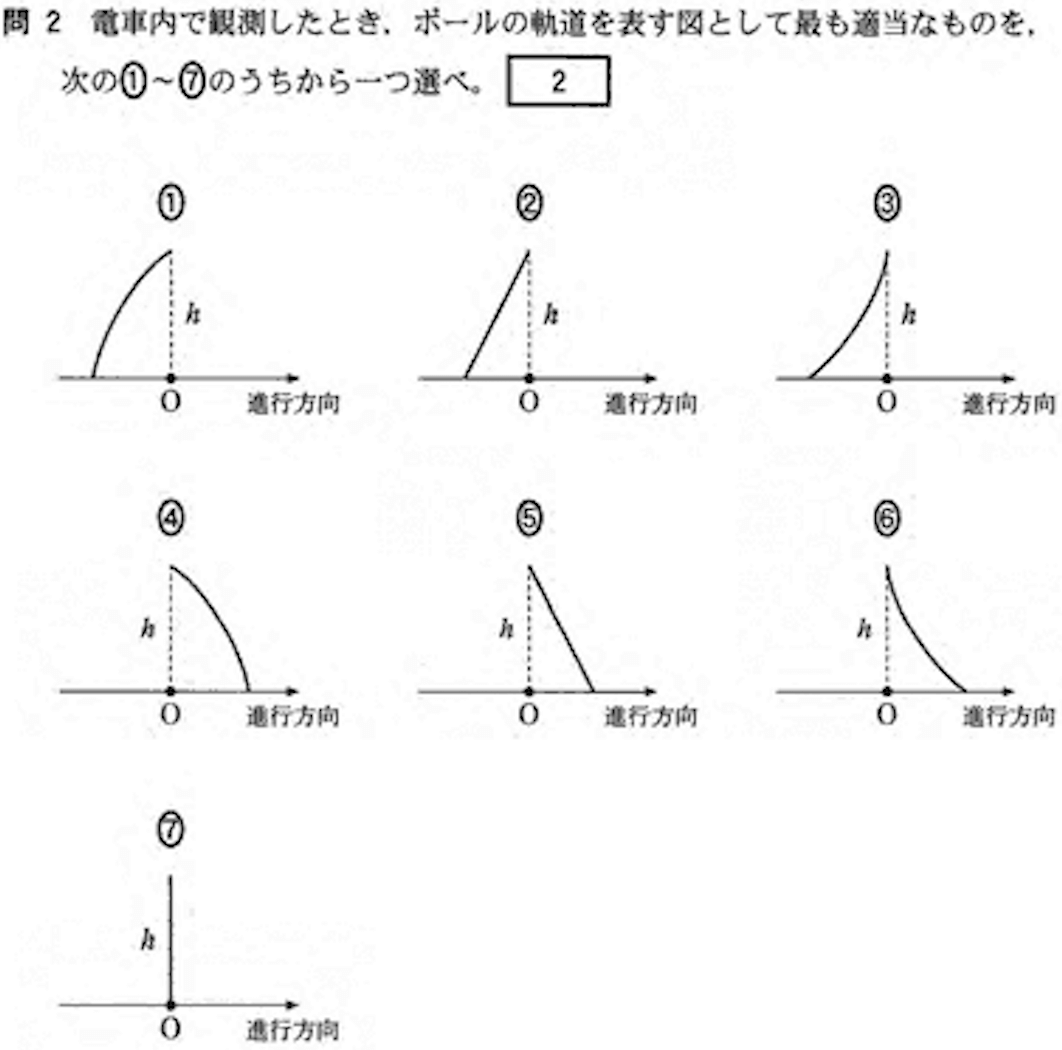
バスの加速度は変化しないので、慣性力の大きさと向きも変化しない。つまり、先ほどの赤い矢印の向きに常に同じ大きさの力が働く。
ボールは静かに(初速度ゼロで)離したので、赤い矢印の向きに等加速度直線運動する。
よって答えは5
問3:力学的エネルギー保存則 答:5
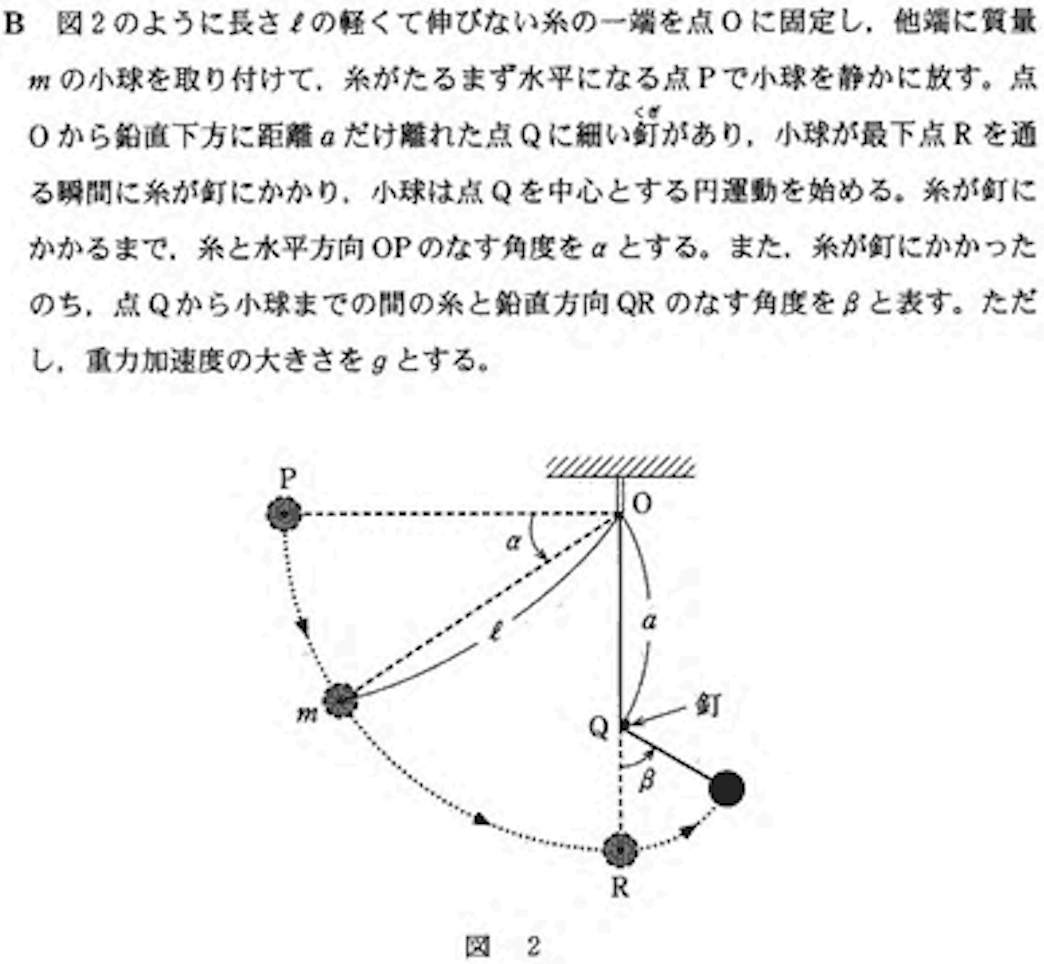

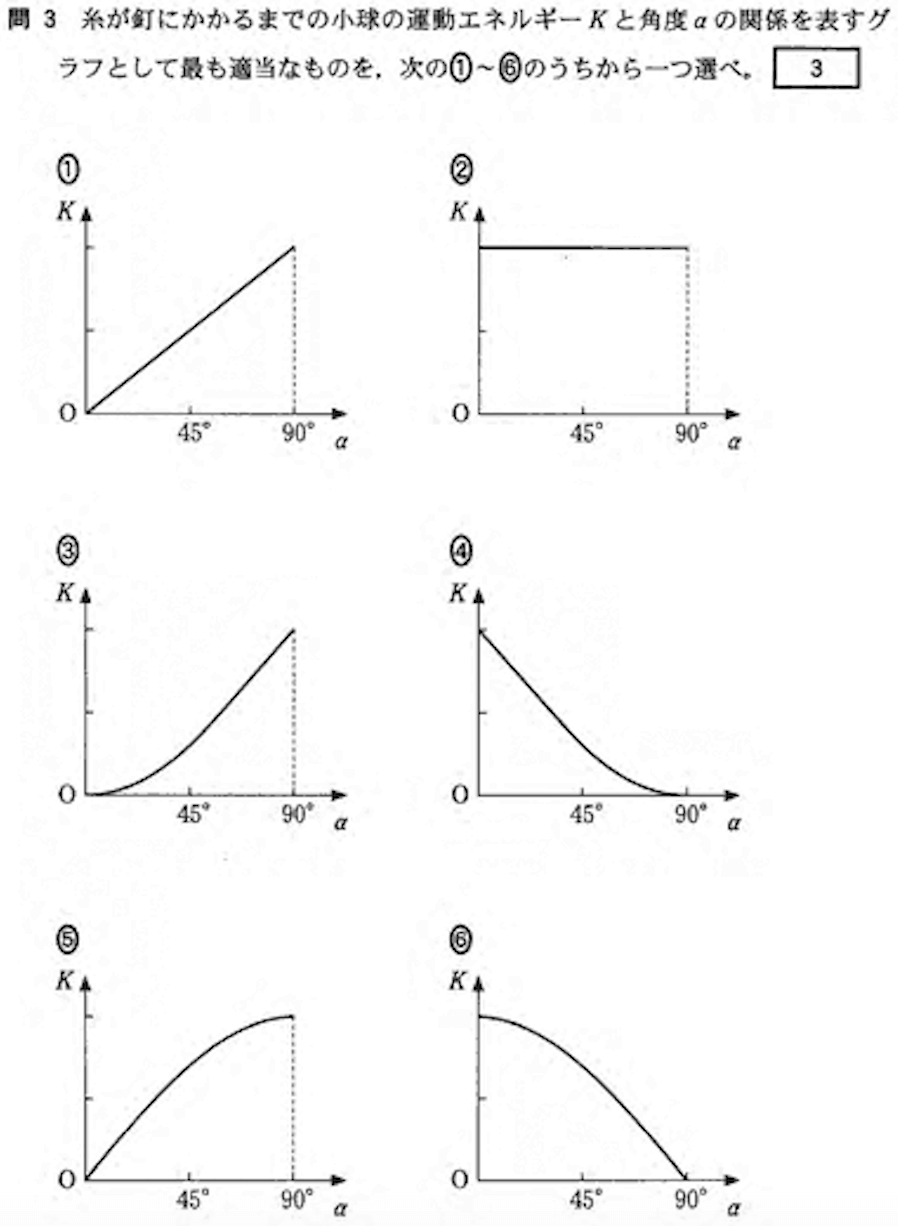

この運動中、非保存力(この状況では張力のみ)は仕事をしないので力学的エネルギーが保存する。
物体が落下すると重力による位置エネルギーが減少し、運動エネルギーへと変化する。
角度\( \alpha \)が小さい時(0°付近)は角度の増加で急激に落下するが、角度\( \alpha \)が大きくなるにつれて落下の仕方は緩やかになる。
つまりはじめのうちは運動エネルギーがゼロから急激に増加し、だんだん緩やかになっていくものを選べばよい。
答えは5
計算でも求めておこう。
角度\( \alpha \)の時の落下距離は\( l\sin{\alpha } \)なので、減少した位置エネルギーは\( mgl\sin{\alpha } \)
これが全て運動エネルギー\( K \)に変換されるので、
これを表すグラフは5
問4:円運動 答:6


\( \beta = 90^{\circ} \)のときも円運動を継続しているので、張力は円運動の遠心力と釣り合っている。(ちょうど90°なので重力は寄与しない)
【公式】円運動の遠心力
円運動しているときに物体が感じる遠心力\( F \)は次のようになる。(等速とは限らない)
\( r \):円運動の半径
\( \omega \):角振動数
\( v \):速さ
遠心力を求めるため、速さ\( v \)を求めよう。
釘にかかった後もエネルギーは保存している。
よってはじめの状態からどれだけ落下したか(位置エネルギーが減少したか)がわかれば、運動エネルギーが求まり速度\( v \)がわかる。
\( \beta = 90^{\circ } \)のとき、
なので、運動エネルギーの公式に代入すると、
\( v \)について解くと、
この円運動の半径は\( l-a \)なので、遠心力\( F \)は、
これが張力と釣り合っているので、張力\( T \)は
よって答えは6


高校物理の家庭教師


最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!