どうも、かきのたねです。
今回はコンデンサーを直列に接続したり、並列に接続したときの合わせた電気容量(合成容量)の計算の仕方を解説します。
抵抗を直列・並列に接続したときの合成抵抗を求めたことはあると思います。コンデンサーの公式はそれとは逆の形をしているので、覚えやすいです。
合成容量を求める手順はたった1つです!
今、理解してしまいましょう。
↓動画版はこちら↓
コンデンサーの電気容量を計算する手順

電気容量とは
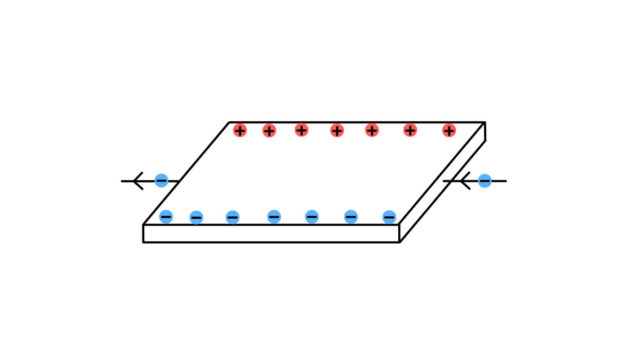
電気を蓄える装置であるコンデンサーを特徴づける量は電気容量だ。ここで電気容量について復習しておこう。
1Vの電圧をかけたときに、コンデンサーに蓄えられる電気量
コンデンサーの電気容量を計算する手順
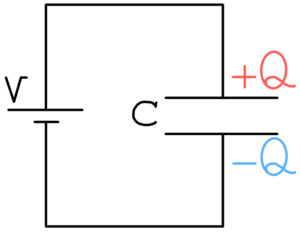
【電気容量を求める方法】
- 電気容量を求めたい(合成)コンデンサーにV[V(ボルト)]の電圧をかける
- 電圧Vを用いて、蓄えられる電気容量Q[C(クーロン)]を計算する
- 電気容量Cは次のようになる。
直列接続したコンデンサーの電気容量
電気容量が\( C_{1},\ C_{2} \)の2つのコンデンサー\( C_{1},\ C_{2} \)を直列につないだときの電気容量を求めよう。
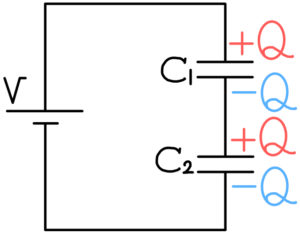
このときコンデンサーをつないでいる部分は電荷0なので、電荷保存則からどちらのコンデンサーにも同じだけの電気量\( Q \)が蓄えられる。
\( Q \)と\( V \)の関係式を求めよう。
コンデンサー\( C_{1} \)にかかっている電圧\( V_{1} \)は
コンデンサー\( C_{2} \)にかかっている電圧\( V_{2} \)は
ここで\( V = V_{1} + V_{2} \)が成り立っていることに注意しよう。
これらを1つのコンデンサーとみなすと、電圧を\( V \)かけて電気量\( Q \)だけ電荷が蓄えられている。
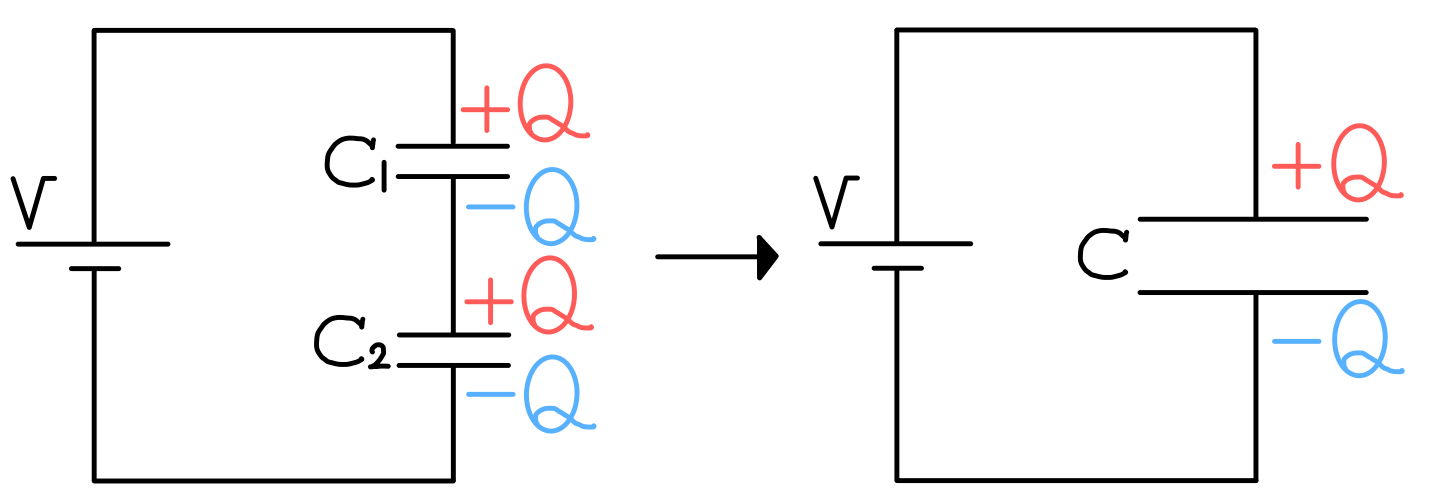

これで直列接続の合成容量\( C \)を求めることができる。
見やすく書き直すと、
並列接続したコンデンサーの電気容量
電気容量が\( C_{1},\ C_{2} \)の2つのコンデンサー\( C_{1},\ C_{2} \)を並列につないだときの電気容量を求めよう。
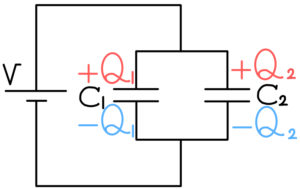


\( Q \)と\( V \)の関係式を求めよう。
コンデンサー\( C_{1} \)に蓄えられた電荷\( Q_{1} \)は
コンデンサー\( C_{2} \)に蓄えられた電荷\( Q_{2} \)は
これらを1つのコンデンサーとみなすと、電圧を\( V \)かけて電気量\( Q = Q_{1} + Q_{2} \)だけ電荷が蓄えられている。
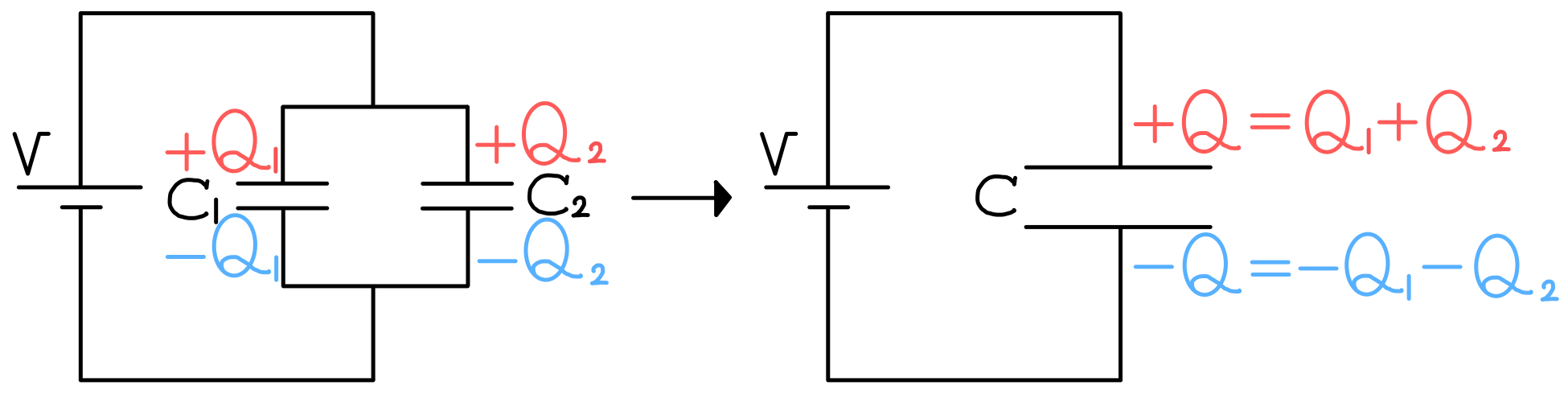

これで並列接続の合成容量\( C \)を求めることができる。
直列接続・並列接続のコンデンサーの電気容量
直列接続



並列接続



「直列は逆数を足して逆数・並列は足すだけ」
もしこの合言葉を忘れてしまっていても、さっき説明したようにすぐ導出できるから心配しないでね!
高校物理の家庭教師


最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!