どうも、かきのたねです。
波の干渉を勉強していると、位相差や経路差がよく出てきますね。今回は位相の基礎と、位相差と経路差の関係について話していきます。
これらはノイズキャンセリング技術などに使われているため、意外と身近なものですね。
位相
物理でよく出てくる波は周期的な運動をしている。
周期的な運動をしているとき、1周期中のどこに対応するのかを表す量として位相というものがある。
例えばシンプルな海の波は、山と谷を交互に繰り返す周期性を持っている。
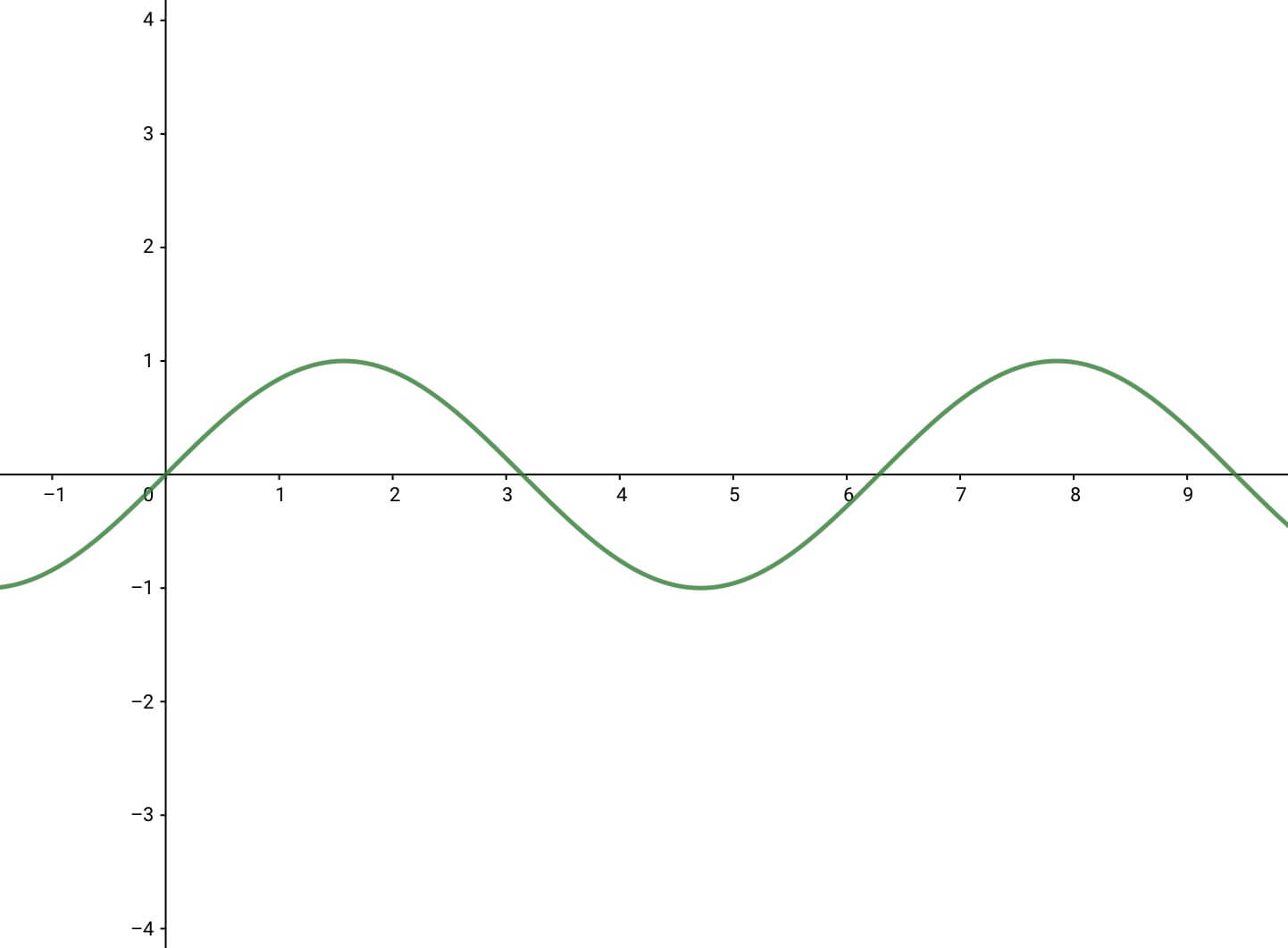
簡単に言ってしまえば、波を\( y=A\sin{x} \)と書いたときの\( x \)を位相と呼んでいる。
上の波で位相\( x=0 \)は変位ゼロ、位相\( x=\frac{\pi}{2} \)は山、位相\( x=\frac{3\pi}{2} \)は谷をそれぞれ表している。(位相\( x=\pi \)は変位ゼロを表すが\( x=0 \)とは振る舞いが違う。)
周期運動の代表例は円運動であり、一回転で\( 2\pi \)回転する。
波の運動や単振動は円運動の見方を変えただけであり、本質的には円運動と大して変わらない。
そのため円運動を基礎として、一周期分に対応する位相は\( 2\pi \)としている。
先ほどの例で言えば位相\( x=\frac{\pi}{2} \)は山を表していたが、一周期分\( 2\pi \)進んだ\( x=\frac{5\pi}{2} \)も同じ山を表す。
同位相、逆位相
周期的な運動をしているとき、現在の状況と一周期分進んだ後の状況は何も変わらない。
このように位相\( 2\pi \)の差があるものは、全く同じものとなる。これらの波を重ね合わせると、波は強め合う。
そのため位相\( 2\pi ( + 2n\pi \ ; \ nは整数) \)の差があるとき、それらを同位相という。
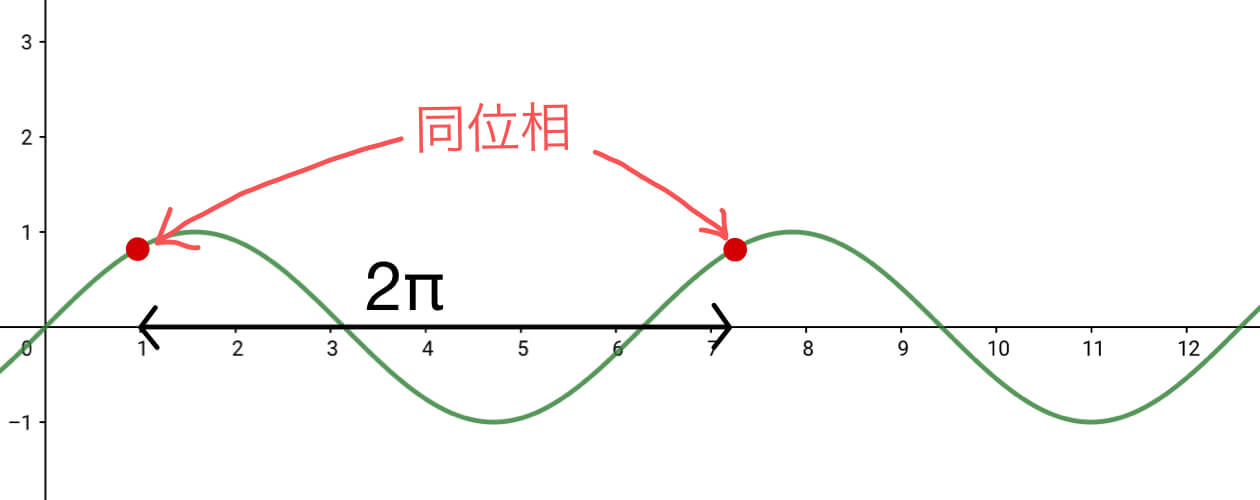
このグラフを見てわかるかもしれないが、位相\( \pi \)だけ差があるところ同士は変位(波の高さ)が逆になっている。例えば山と谷は、一方が変位\( 1 \)もう一方が変位\( -1 \)である。
これらのように位相\( \pi ( + 2n\pi \ ; \ nは整数) \)の差があるとき、それらを逆位相という。
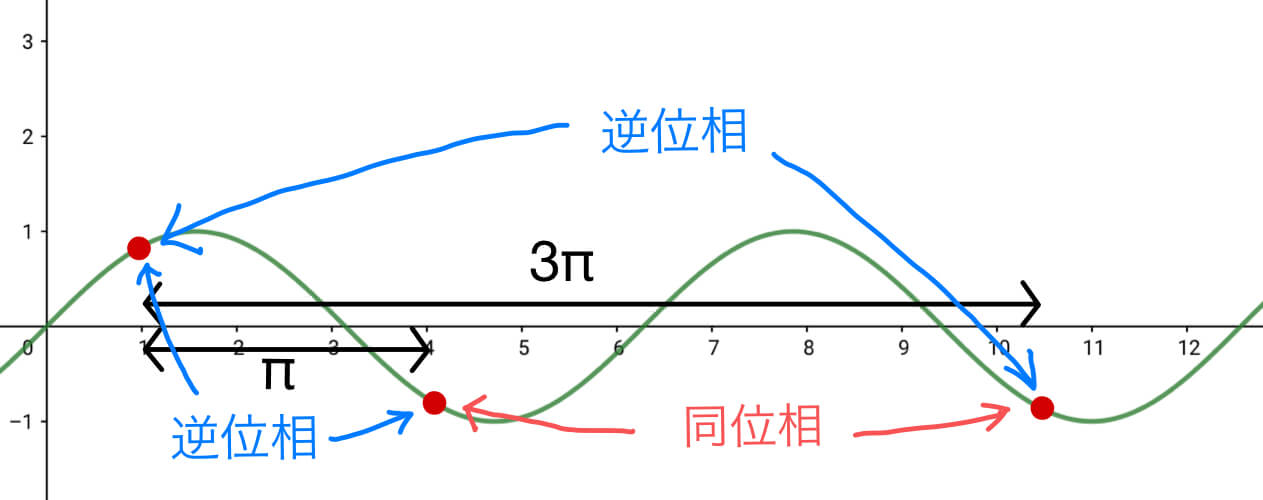
逆位相の関係にある変位を合成(足す)と、もちろん打ち消しあう(弱めあう)。これを応用したのがノイズキャンセリングだ。
ヘッドホンなどに内蔵されたマイクが周囲の音を拾い、その音の波形を瞬時に読み取って逆位相の音を一緒に流しているのだ。
経路差による強めあいと弱めあいの判定
位相差と経路差の関係
光などの波は速さが一定なので、位相(1周期中のどこに対応するか)は波の進んだ長さ\( l \)で測ることができてしまう。
- 1周期(位相\( 2\pi \)分)進めば\( l=\lambda \)分だけ波は進む。
- 半周期(位相\( \pi \)分)進めば\( l=\frac{\lambda}{2} \)分だけ波は進む。
- \( \frac{1}{4} \)周期(位相\( \frac{\pi}{2} \)分)進めば\( l=\frac{\lambda}{4} \)分だけ波は進む。
つまり位相\( \theta \)分波が進めば波は距離\( l=\lambda \frac{\theta}{2\pi} \)進む。
逆に波が距離\( l \)進むと位相\( \theta =2\pi \frac{l}{\lambda} \)分だけ波が進んでいるとわかる。
同位相なのか逆位相なのかは位相差で測っていたので、位相差の代わりに経路差から同位相なのか逆位相なのかを判別できてしまうのだ。
ここまで理解したところで、波の干渉についてまとめよう。
簡単のため互いに同位相で出された波についてまとめる。
波の干渉:位相差による判定
強めあい(同位相)
位相差:\( \Delta \theta = 2\pi + 2n\pi \)
弱めあい(逆位相)
位相差:\( \Delta \theta = \pi + 2n\pi \)
波の干渉:経路差による判定
強めあい(同位相)
経路差:\( \Delta l = n\lambda \)
弱めあい(逆位相)
経路差:\( \Delta l = ( n + \frac{1}{2} ) \lambda \)
まとめ
周期的な運動をするものが、ある瞬間に1周期中のどこに対応する運動をしているのかを表す量が位相である。
この位相を使えば、重ね合わせた波が強めあうのか弱めあうのかが判別できる。
進む速さが一定の波は経路差で位相差を測ることができ、位相差の代わりに干渉の仕方を経路差で測ることができる。
高校物理の家庭教師

最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!