どうも、かきのたねです。
今日はセンター試験でしたね。今回は2019年度のセンター物理をわかりやすく解説していきます。
まず第1問から。





問1:運動エネルギーと運動量 答:2

- エネルギーは向きをもたない。
- 例えば同じ大きさの粘土を同じ速さで正面衝突させた場合、くっついて速度はゼロになる。つまり運動エネルギーを完全に失ってしまう。一般に弾性衝突でなければエネルギーは保存しない。
- 力積は、運動量変化と等しい。
- 運動量は大きさと向きをもつ。等速円運動では運動量の大きさは変化しないが、常に向きが変わっている。
正しいのは2
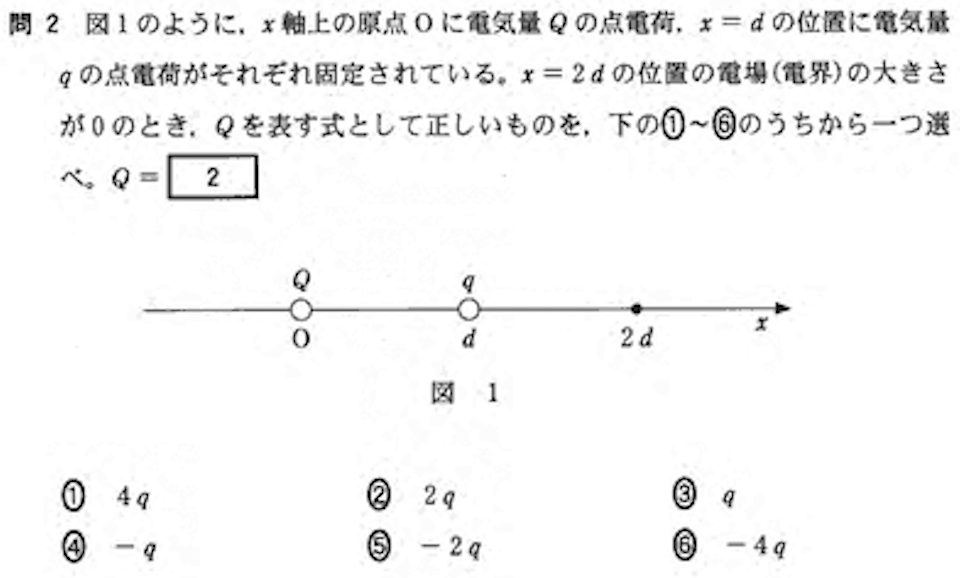
問2:点電荷のつくる電場 答:6

【公式】点電荷の作る電場の大きさ
電気量\( Q \)の点電荷が距離\( r \)離れた位置につくる電場の大きさ\( E \)は、次のように表せる。(\( k \):比例定数)
\( q \)が位置\( x = 2d \)につくる電場\( E_{q} \)は、右向きを正として、
\( Q \)が位置\( x = 2d \)につくる電場\( E_{Q} \)は、右向きを正として、
これらを合わせると位置\( x = 2d \)の電場がゼロになるので、
これを\( Q \)について解くと、
となり、答は6
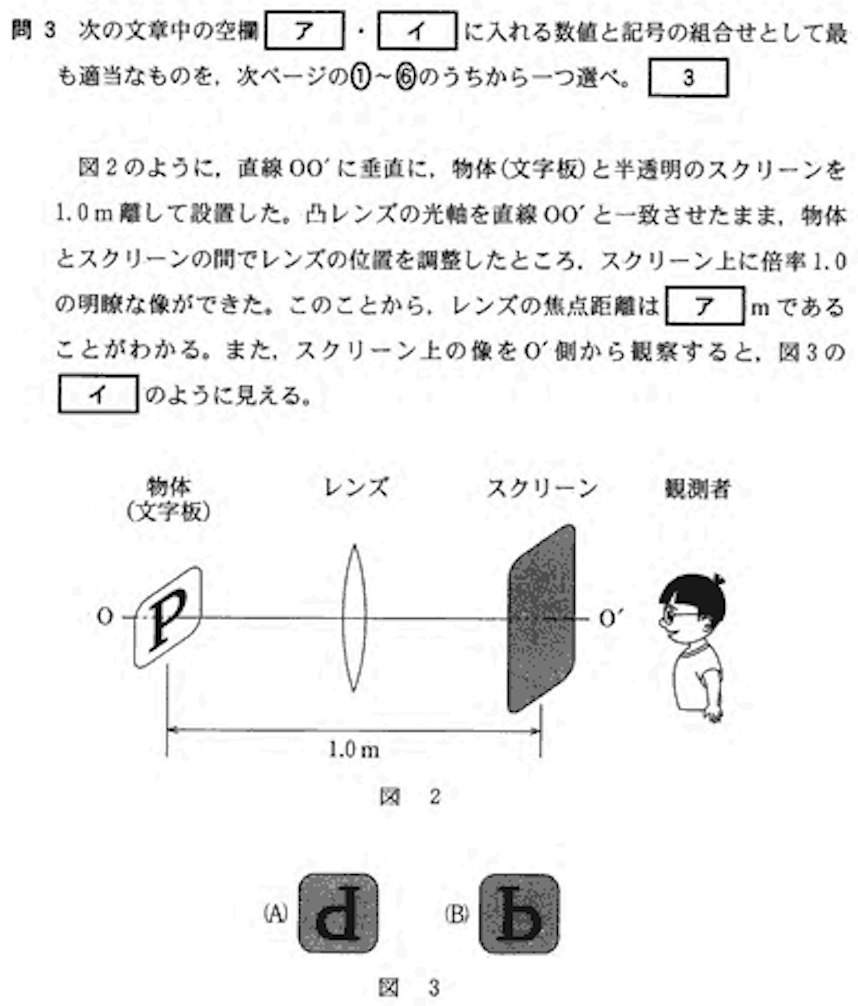
問3:レンズによる実像 答:1


【公式】レンズの公式
\[ \frac{1}{a} + \frac{1}{b} = \frac{1}{f} \]
\( a \):レンズから物体までの距離
\( b \):レンズから像までの距離
\( f \):焦点距離
この問題の設定では、
ですね。
これをレンズの公式に代入すると、
と計算できます。
実像は上下左右反転してスクリーンに映るので、このようになる。


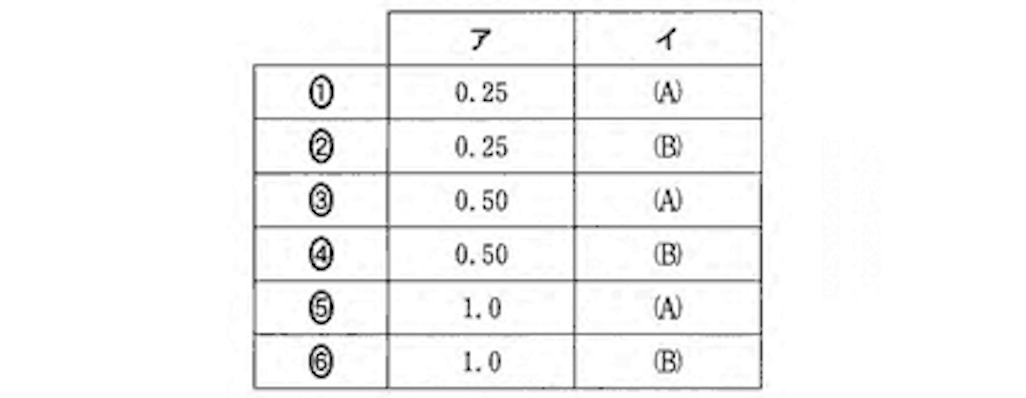
ア:0.25m, イ:(A) なので、答は1
問4:気体の状態方程式 答:5


シリンダー内の気体にかかる力\( F \) = 外気の圧力 + ピストンの重さ
これを式にすると、
気体は圧力\( P \)でピストンを押し返すとする。この圧力による力\( PS \)が今求めた力と一致する(\( PS = F \))ので、
これを気体の状態方程式\( PV = nRT \)に代入しよう。(\( V = Sh \))
よって答は5
問5:単振動 答:4
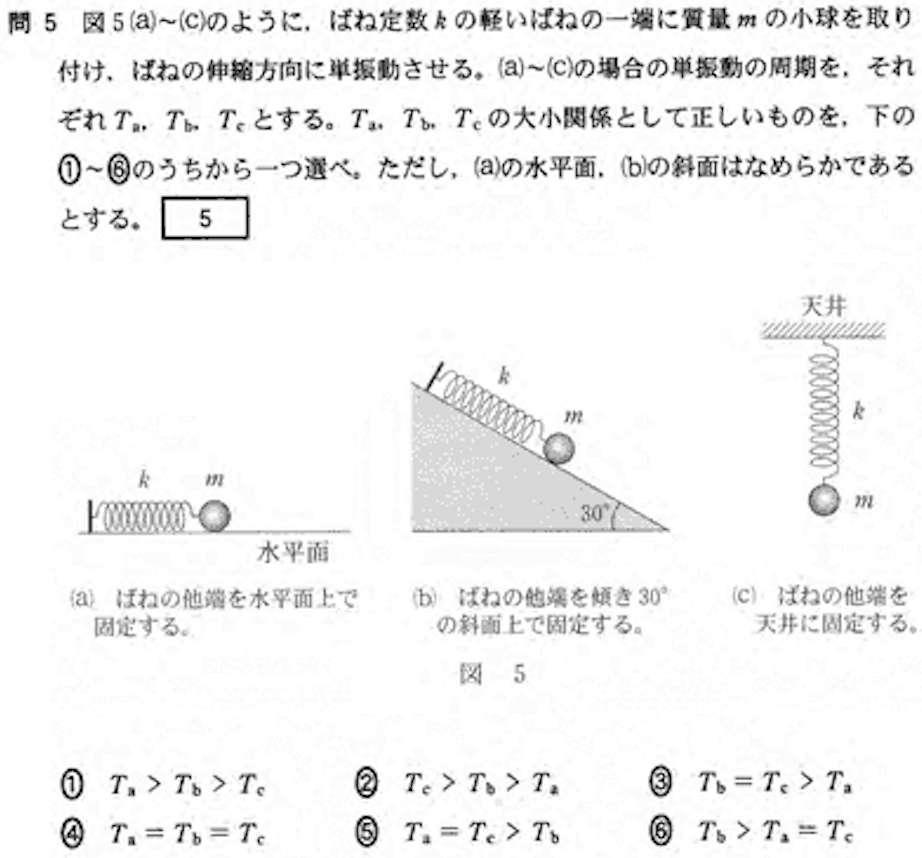

バネによる単振動は物体の質量とバネ定数のみによって決まることを知っていれば、答が4であることはすぐにわかる。
計算で確認してみよう。
【公式】単振動の公式
加速度\( a \)が変位\( x \)を使って次のように表せるとき、その物体は単振動する。
\[ a = – K ( x – x_{0} ), \ K > 0 \]
\( K \):\( K=\omega ^{2} \)と書けば、\( \omega \)は角振動数である。
\( x_{0} \):単振動の振動中心
さらに角振動数\( \omega \)と周期\( T \)には次の関係がある。
(a)~(c)の運動方程式から、変位\( x \)の時の加速度を求めよう。
(a)水平面で振動


物体にかかる力:\( F = -kx \)
運動方程式:\( ma = -kx \)
加速度:\( a = – \frac{k}{m} x \)
これは角振動数\( \omega = \sqrt{\frac{k}{m}} \)・振動中心\( x = 0 \)の単振動を表す。
よって、\( T_{a} = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{m}{k}} \)
(b)斜面で振動
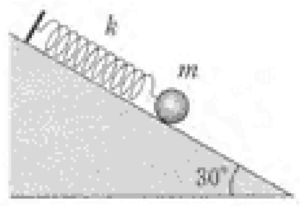

物体にかかる力:\( F = -kx + \frac{mg}{2} \)
運動方程式:\( ma = -kx + \frac{mg}{2} \)
加速度:\( a = – \frac{k}{m} ( x- \frac{mg}{2k} ) \)
これは角振動数\( \omega = \sqrt{\frac{k}{m}} \)・振動中心\( x = \frac{mg}{2k} \)の単振動を表す。
よって、\( T_{b} = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{m}{k}} \)
(c)天井に吊るされて振動


物体にかかる力:\( F = -kx + mg \)
運動方程式:\( ma = -kx + mg \)
加速度:\( a = – \frac{k}{m} ( x- \frac{mg}{k} ) \)
これは角振動数\( \omega = \sqrt{\frac{k}{m}} \)・振動中心\( x = \frac{mg}{k} \)の単振動を表す。
よって、\( T_{c} = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{m}{k}} \)
(a)~(c)からわかること
- 単振動の周期(や角振動数)は、バネ定数と物体の質量のみによる。
- 重力がどれだけ働いているかで、単振動の振動中心が異なる。
以上より、答が4であることが確かめられる。
これだけは忘れないようにしましょう。
まとめ
第1問は、物理をやっているなら絶対に覚えておく必要のある知識を問う問題でしたね。
高校物理の家庭教師


最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!