どうも、かきのたねです。
「コンプトン効果がよくわからない」
「計算がうまくいかない」
「そもそもなんでこんな実験が必要なのかわからない」
そんな人、多いと思います。
今回はそのコンプトン効果について、わかりやすく解説していきます!
コンプトン効果ってどんな現象?
まずコンプトン効果とはどのような現象なのか見ていこう。
この現象は意外と単純で、「物体に光を当てると、角度によっては波長が少しだけ長くなって散乱される現象」だ。

しかもこの波長の変化は、「当てる光の波長」や「光が当たる物体」に依存せず、散乱される角度のみに依存するという面白い現象。
散乱された方向によって波長が異なることは、実は量子論でないとうまく説明できない。
量子論でないと説明できない理由
光って何だろう?
なぜ量子論でなければ説明できないのかというと、「量子論抜きでは、散乱で光は波長を変えない」のだ。
まずは、そもそも散乱とはどんな現象なのか見ていこう。
光 = 電磁波
ということは聞いたことがある人も多いだろう。では電磁波とは何か。
電磁波 = 電場と磁場の振動
空間内に分布する電場と磁場の振動が、光の正体である。目(網膜)に届いた電場と磁場の振動を、人間は光として認識しているのだ!
人の目はすごくて、可視光の範囲外の電磁波は認識しないんだ。例えば携帯の電波とかは見えないよね。
光の散乱
電子による光の散乱を考えよう。
- STEP01電子に光が当たる電子に光(電磁波)が当たると、その電子は電磁波に合わせて振動する。
- STEP02電磁波の発生電子が振動することで、電子の作っていた電場が振動し、また磁場も振動する。
- STEP03電磁波の放射その振動(電磁波=光)が周囲に伝わっていく。
ここで注意したいのは、入射した光の振動数と散乱した光の振動数が変わらないことだ。この過程では振動数は変化できない。
量子論による説明
光量子仮説
では量子論でどのように説明されるのか、見ていこう。
量子論では、光はエネルギーと運動量を持った粒の集まりだと考える。
振動数\( \nu \)、波長\( \lambda(=\frac{c}{\nu}) \)の光1粒のエネルギー\( E \)と運動量\( p \)は、プランク定数と呼ばれる非常に小さな定数\( h \)を使って次のように表せる。
\[ E = h\nu,\ p = \frac{h}{\lambda} \]
コンプトン効果
光量子仮説を使うと、コンプトン効果をうまく説明できる。
原因を簡単に言ってしまえば、「光が当たった粒子は弾き飛ばされていることを考えていなかった」ということだ。光が当たったら振動すると考えていたが、実は少しだけ並進運動もしていたのだ。
質量\( m \)の粒子に光1粒(波長\( \lambda \))が当たり、粒子が速さ\( v \)、波長\( \lambda^{\prime} \)で飛ばされる状況を具体的に考えてみよう。
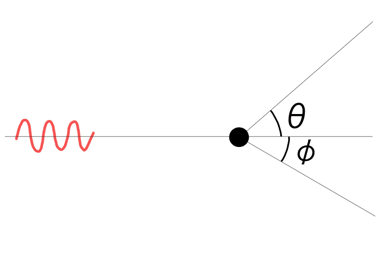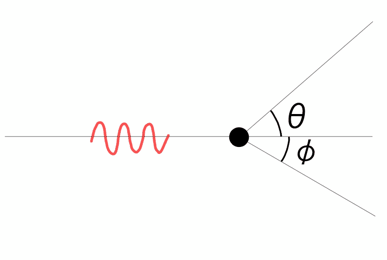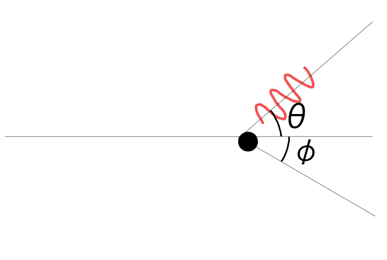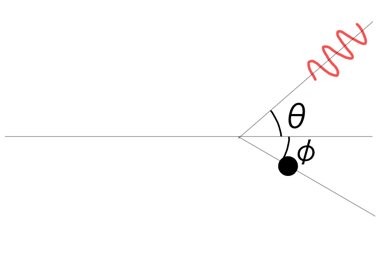

エネルギー保存則
\[ \frac{hc}{\lambda} = \frac{hc}{\lambda^{\prime}} + \frac{1}{2}mv^{2} \]
運動量保存則
\[ x方向\ :\ \frac{h}{\lambda} = \frac{h}{\lambda^{\prime}}\cos{\theta} + mv\cos{\phi} \]
\[ y方向\ :\ 0 = \frac{h}{\lambda^{\prime}}\sin{\theta} – mv\sin{\phi} \]
これらの式から\( \lambda – \lambda^{\prime} \)を求めてみよう。まず運動量保存則の2つの式を使って\( \phi \)を消去する。
\[ \left( mv \right) ^{2} = \left( \frac{h}{\lambda} \right)^{2} – 2\frac{h^{2}}{\lambda \lambda^{\prime}}\cos{\theta} + \left( \frac{h}{\lambda^{\prime}} \right)^{2} \]
この式とエネルギー保存則の式を使って\( v \)を消去する。ここで\( \frac{\left( \lambda^{\prime} – \lambda \right)^{2}}{\lambda \lambda^{\prime}} \)はとても小さいとして近似する。
\[ \lambda^{\prime} – \lambda = \frac{h}{mc} \left( 1 – \cos{\theta} \right) \]
これが求めたかった式だ!当てている光の波長や光が当たる物体に依存していない。
この式から、量子論を使えば光の波長が伸びることを説明できることがわかった。
高校物理の家庭教師


最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!