どうも、かきのたねです。
コンデンサーに誘電体を挿入するととても複雑に見えますよね。
極板間に隙間なく誘電体が挿入されているならまだ比較的簡単かもしれないけど、一部分にしか挿入されていなかったりする。
そこで日々高校生や大学生たちに物理を教えている私かきのたねが、コンデンサーの極板間に誘電体を挿入したらどうなるのか解説します!
多くの人がつまづいてしまうこの問題。今ここで理解しましょう!!
コンデンサーに誘電体を隙間なく挿入
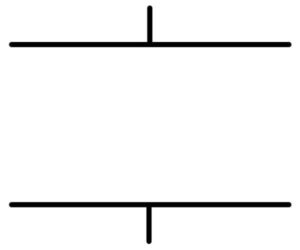
真空中にこのような、極板間距離\( d \)のコンデンサーがあるとしよう。極板間には何もない。
この極板間に誘電体を挟み込む。
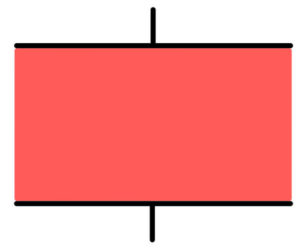
このままではただ極板間に誘電体があるだけだ。
しかしこれに電圧をかけると話は変わってくる。
ただの何もないコンデンサーに電圧\( V \)をかけてみよう。すると電荷\( Q \)貯まる。
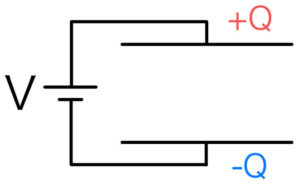
どれだけの電荷が貯まるのかは、かけた電圧\( V \)で決まるのだった。(\( Q=CV \))

ここでのポイントは、電荷が貯まると極板間に電場ができ、この電場による電位差が\( V \)となるということだ。
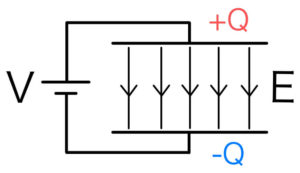
電位差が\( V \)となるような電場を作るために電荷\( Q \)が貯まると言ってもよい。
ここに誘電体を挿入するとどうなるだろうか?
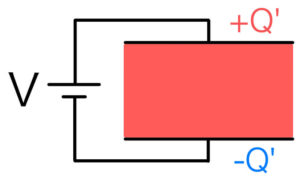
この分極によって誘電体内部の電場が弱められるのだ。
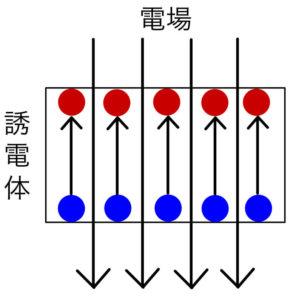
電場が弱まるとどうなるか?
この電場によって作られる電位差も小さくなってしまうから、電位差が\( V \)となるように追加で電荷が貯まることになる。
ちなみに極板間距離は変わっていないので、元の電場と同じ電場(\( E’=E \))になるように電荷\( Q’ \)が貯まる。(\( Q’>Q \))
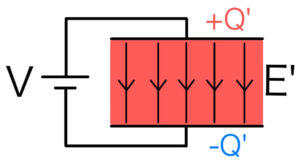
ここからは具体的に数式を使って、この誘電体を挿入したコンデンサーの電気容量を求めよう!
比誘電率\( \epsilon_{r} \)の誘電体の中では、電場の大きさは\( \frac{1}{\epsilon_{r}} \)倍される。
そのため極板間電位差も\( \frac{1}{\epsilon_{r}} \)倍されることになる。
もともと電位差が\( V \)となるっていたのが、\( \frac{V}{\epsilon_{r}} \)になってしまう。これを電源の電位差\( V \)に戻すために何が起こるか?
蓄えられる電荷が増えるのだった。
電場の大きさは蓄えられた電荷に比例するので、電荷が\( \epsilon_{r} \)倍されることで電位差の減少を打ち消すのだ!
電気容量とは「1ボルトあたりに蓄えられる電気量」であった。つまり蓄えられた電気量が\( \epsilon_{r} \)倍されたので、電気容量も\( \epsilon_{r} \)倍される。
元の電気容量を\( C \)とすると、
コンデンサーの下側に誘電体を挿入
次はコンデンサーの下側に誘電体を挿入したときに、電気容量がどう変化するのかを考えよう。誘電体の幅は\( b \)、上側の空の部分の間隔は\( a \)とする。
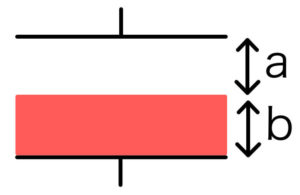
電気容量を求めたいので、電圧Vの電源に接続しよう。
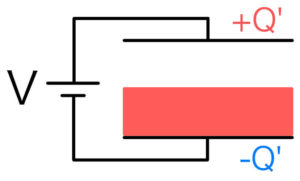
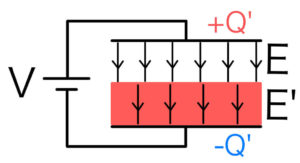
先ほどと同じように、下側では電場が弱められてしまう。そのため蓄えられる電荷は増えるのだった。
どれだけ電荷が貯まるかというと、極板間の電位差が\( V \)になるまで貯まる。
そのため先ほどよりは小さいが、電気容量が増えることは予想できるだろう。具体的に計算してみよう!
計算は次のように進める。
電気容量の計算法
- 電荷\( Q’ \)が蓄えられているとして、極板間の電位差を求める。
- この電位差が電源の電圧\( V \)となるような\( Q’ \)を求める。
- \( Q’ \)を\( V \)で割り算して、\( C(=\frac{Q’}{V}) \)が求まる。
極板間の電場を求める
このコンデンサーの上側のように極板間に何もなければ、そこでの電場\( E \)は
このコンデンサーの下側のように極板間が誘電体(比誘電率\( \epsilon_{r} \))で満たされていれば、そこでの電場\( E’ \)は
極板間の電位差を求める
上側の間隔が\( a \)、下側の間隔が\( b \)なので、極板間の電位差は
電気容量を求める
これが電源の電位差\( V \)となればいいので
これで\( Q’, \ V \)の関係がわかったので、\( C=\frac{Q}{V} \)から電気容量を計算できる。
より見やすく書き直すと、
これをよく見ると、何も挿入されていない極板間距離\( a \)のコンデンサーと誘電体を挿入した極板間距離\( b \)のコンデンサーを直列に接続したものと全く同じことがわかる。


なぜ直列接続と同等なのか
これは誘電体の上面の電位が一定なので、そこに薄い金属板を挿入しても極板間の電場が変わらないことから理解できる。



重要だったのは電位差を作り出す電場だった。
この電場の分布が変わらなければ電位差も変わらないので、電気容量が変わらないのだ。
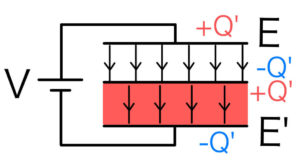

この金属板をさらに薄く切り離して導線で繋いでも、極板間の電場の分布は変わらない。
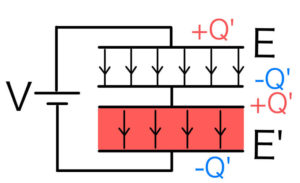

コンデンサーの下側に誘電体を挿入したものは、図のように2つに分離して直列に接続したものと全く同じになってしまうことがわかっただろう。
でももし表面の電位分布にムラがあった場合、薄い金属板内の電位を一定にするために金属表面の電荷が移動して、電場の分布が変わってしまうよ。
電場が変わるともちろん電位差も変わってしまうから、薄い金属板を置いた時点でコンデンサーの電気容量は変わっちゃうんだ。
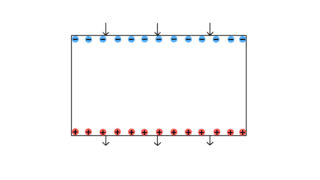

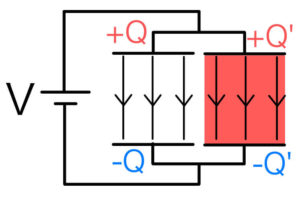
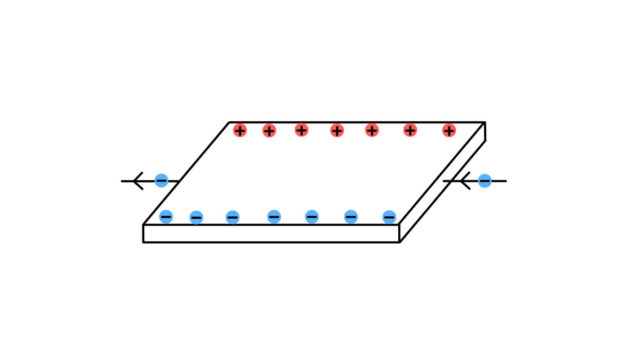
コンデンサーの右側に誘電体を挿入
次はコンデンサーの右側に誘電体を挿入したときに、電気容量がどう変化するのかを考えよう。右側の誘電体の底面積はS’、左側の空の部分の底面積はSとする。
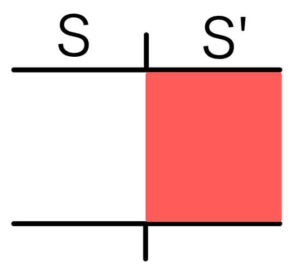

電気容量を求めたいので、電圧Vの電源に接続しよう。
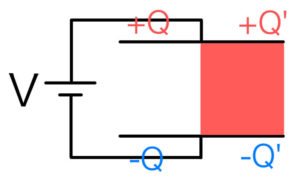

誘電体を挿入した直後は、その部分で誘電体が分極して電場が弱められるのであった。
この右側の弱まった電場を強めて電位差を電源の電圧\( V \)と合わせるように、右側にだけ追加で電荷がたまる。
誘電体による電場の弱まり方は先ほどと同様\( \frac{1}{\epsilon_{r}} \)倍なので、それを補うように右側の電荷は\( \epsilon_{r} \)倍となる。
これを数式にして、電気容量を求めよう!
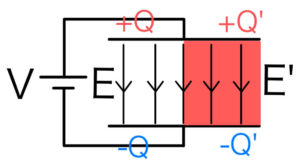


計算は先ほどと同じように、次のように進める。
電気容量の計算法
- 左側に電荷\( Q \)、右側に電荷\( Q’ \)が蓄えられているとして、極板間の電位差を求める。
- この電位差が電源の電圧\( V \)となるような\( Q, \ Q’ \)を求める。
- コンデンサーに貯えられた電荷\( Q+Q’ \)を電源の電圧\( V \)で割り算して、\( C\bigl(=\frac{Q+Q’}{V}\bigr) \)が求まる。
極板間の電場を求める
このコンデンサーの左側のように極板間に何もなければ、そこでの電場\( E \)は
このコンデンサーの右側のように極板間が誘電体(比誘電率\( \epsilon_{r} \))で満たされていれば、そこでの電場\( E’ \)は
極板間の電位差を求める
左側の極板間の電位差は
右側の極板間の電位差は
電気容量を求める
これらはそれぞれ電源の電圧\( V \)と等しくなるので、
これら電荷と電圧の関係式から、\( C\bigl(=\frac{Q+Q’}{V}\bigr) \)が求まる。
これをよく見ると、何も挿入されていない極板面積\( S \)のコンデンサーと誘電体を挿入した極板面積\( S’ \)のコンデンサーを並列に接続したものと全く同じことがわかる。


なぜ並列接続と同等なのか
これはコンデンサーを縦に分割しても、極板間の電場が変わらないことから理解できる。



もともとこのような分布だったものが、分割されると次のようになる。

端での電場の乱れは無視していて縦方向にしか向いていないので、縦に切って2つに分離しても何も変わらないのだ。
コンデンサーの右下に誘電体を挿入
問題
最後に、コンデンサーの右下に誘電体を挿入したらどうなるのか考えよう。
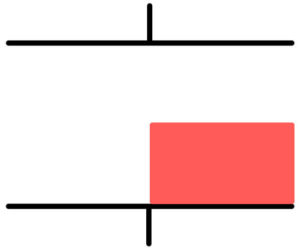

これは次の2つの接続A,Bのうち、どちらかと等価である。
A
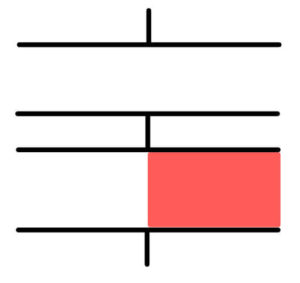

B
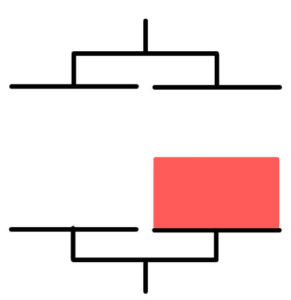

ここまでの説明を聞いていれば理解できるはずだ。
ヒントは「等価であるとは、電場の分布が変わらないこと」だ。(※ヒントは白塗りにしているよ)
答え合わせ
では答え合わせをしよう。
正しいのはB。Aは間違っている。
電場の分布に注目しよう。
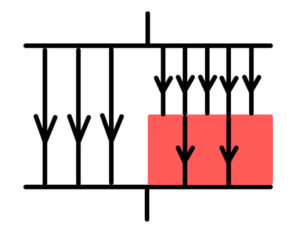

右側には誘電体があるため、誘電体挿入前よりも多くの電荷が貯まらなければならない。
そのせいで右側の真空部分は、電場が強くなる。電荷の増加に伴って誘電体部分も電場は強くなるが、元の電場よりは弱い。
これを図で表したのが上の図である。AとBの2つのパターンで電場の分布が同じになれるものはどちらか?
このまま分割して描いてみよう。
A
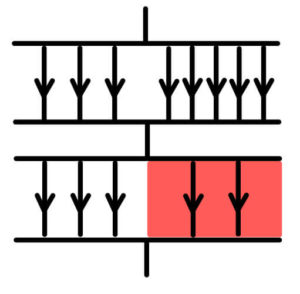


B
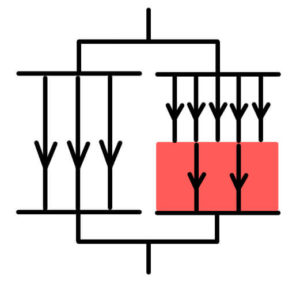

電場の分布が縦方向だったので、Bは何も変わらない。
しかしAは大きな誤りがあることに気づいただろうか。



上の何も挿入されていない上側のコンデンサーに注目。右側と左側で電場の大きさが違う。そのため左右で電位差が違うのだ。(下側も左右で電位差が違う)
これでは金属板(上側のコンデンサーの極板)の電位が左右で違ってしまうことになる。
金属を電位差のある空間に置くと、その電位差を打ち消すように電荷が勝手に移動してしまう。そのせいでAに描いた状態は安定でなく、金属内の電位差をなくすように電荷が移動し、電場の分布が変化することになる。
よって正しいのはB
- 下側(や上側)に誘電体が挿入されている
- 右側(や左側)に誘電体が挿入されている
ようなコンデンサーの電気容量が、直列接続・並列接続されたコンデンサーと同等である理由をしっかりと理解すれば、意外と簡単にわかってしまうんだ。
コンデンサーを扱うときは、極板間の電場がどうなるのかを考えると簡単に理解できることが多いよ!
高校物理の家庭教師


最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!







コンデンサーの電場のところ
誘電率εr❌ 比誘電率εr⭕
だと思います。
ご指摘ありがとうございます。
誤字であることが確かめられたため訂正いたしました。
73才の独習生です。並行接続コンデンサでスイッチオフ後誘電体入れて電圧が減って充電量の再配置がされる訳を色々なサイト巡りしましたが、誘電体の電気力線の矢印で電位差が少なくなるあなた様のサイトに巡り会いました。誘電体がはいると電位差が減るので電池がそのままなら多くの電荷が蓄えられ、電池のエネルギーがないオフの状態だと誘電体が入ったほうが電位が下がり結果入れなかった方も含め全体の電位再配置が起こるのでしょうか?東北大経済出身1972年卒
コメントありがとうございます。
初めに結論を言いますと、あなたの理解は正しいです。
簡単に時系列を考えてみます。
(1)2つのコンデンサーが並列接続されている。(両方のコンデンサーの極板間電圧が同じ)
(2)片方に誘電体を挿入する。
(3)誘電体挿入側の極板間電圧が減少する。
(4)並列接続されているため、2つのコンデンサーの電圧が同じになるように電荷が移動する。
(5)並列接続されたコンデンサーの極板間電圧は、誘電体挿入前に充電が完了した(1)での電圧よりも減少している。
以上のことから、2つのコンデンサーそれぞれに蓄えられた電荷が移動することが理解できると思います。
コンデンサー間で電荷が移動しただけで、2つのコンデンサーに蓄えられた電荷の合計量は変化していません。
しかし(5)のとおり、電圧は減少しています。
この状態でスイッチをONにして同じ電源に繋ぐと、(1)と同じ電圧になるまで追加で充電されます。
誘電体を挿入したことでより多く充電できることになるのです。