どうも、かきのたねです。
交流回路にコイルやコンデンサーを接続すると、電流の変化と電圧の変化に差が生じます。これを「電圧の位相は、電流の位相よりも進んでいる(遅れている)」と言っているのを聞いたことがあるかもしれません。
今回はこの交流回路での位相のずれについて説明していきます!
位相がわからない人は↓こちらを読んでみてください。
電流と電圧の関係(イメージ)
抵抗は同位相
ここでは抵抗での電流と電圧の関係(オームの法則)について復習するので、時間のない方は次の見出しまで進んでください。
抵抗に電圧をかけると電流が流れるが、これらの間にはオームの法則が成り立っている。
\[ V=RI \]
これから解説するコイルやコンデンサーについて理解しやすくする為に、交流回路での抵抗について見ていこう。
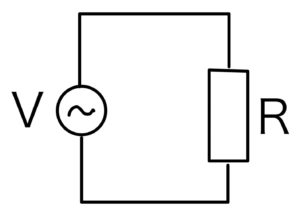
抵抗に
\[ v=V_{0}\sin{\omega t} \]
(\( V_{0} \)は振幅、\( \omega \)は角振動数(角周波数))の電圧をかけたとしよう。この抵抗にはどのような電流が流れるだろうか?
オームの法則を使えば簡単だ。
\[ i=\frac{v}{R}=\frac{V_{0}}{R}\sin{\omega t} \]
\( v \)と\( i \)を比べてみるとわかるが、これらは同位相(sinの中身\( \omega t \))だ。
電流\( i \)と電圧\( v \)をグラフに描いてみよう(電流と電圧は違う物理量なので同じグラフにしてしまうのはあまり良くないので注意)。
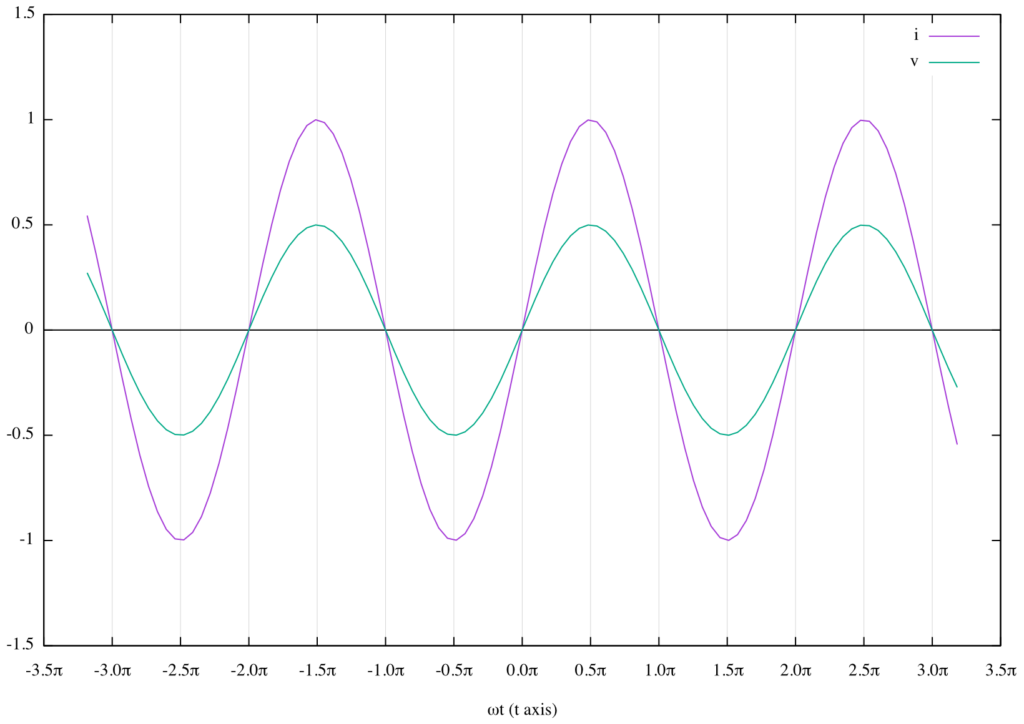
山や谷の位置がどちらも同じであることに気がつくだろう。コイルやコンデンサーだと違いが出てくる。
コンデンサーで電圧の位相が\( \frac{\pi}{2} \)遅れる理由
次に電気容量が\( C \)のコンデンサーに交流電圧\( v=V_{0}\sin{\omega t} \)をかけたときに、どのような電流が流れるか考えてみる。
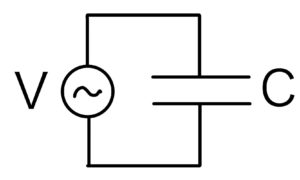
コンデンサーでは次の公式が成り立つことを思い出そう。
\[ Q=Cv \]
これは電圧\( v \)がかかったときにどれだけ電荷\( Q \)が溜まるのかを表わしている。
ところで電流は電荷の流れだったので、電流が流れているとコンデンサーに電荷が溜まっていく。上の式のようにコンデンサーの電荷と電圧は比例しているので、つまり電流が正ならば電圧が増えていくのだ。
グラフで見やすいように言い換えると、電流が正のとき電圧のグラフの傾きが正となる。ついでに言うと、コンデンサーに流れ込む電流が大きければ大きいほど電圧のグラフの傾きは急になる。
これをグラフにしてみよう。
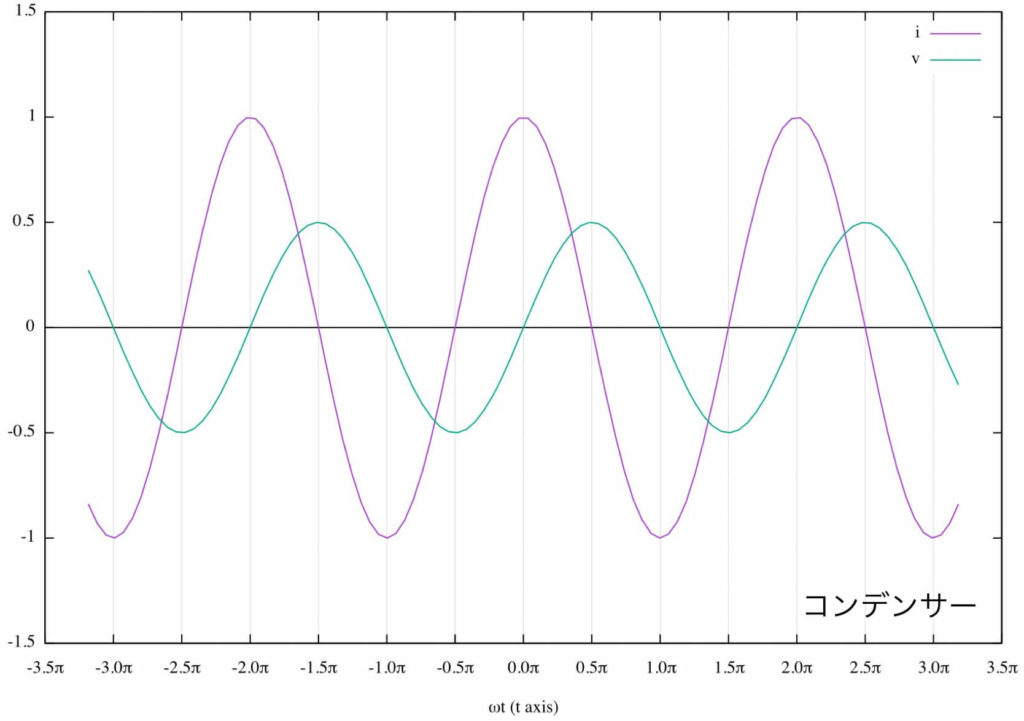
これに説明を加えておく。
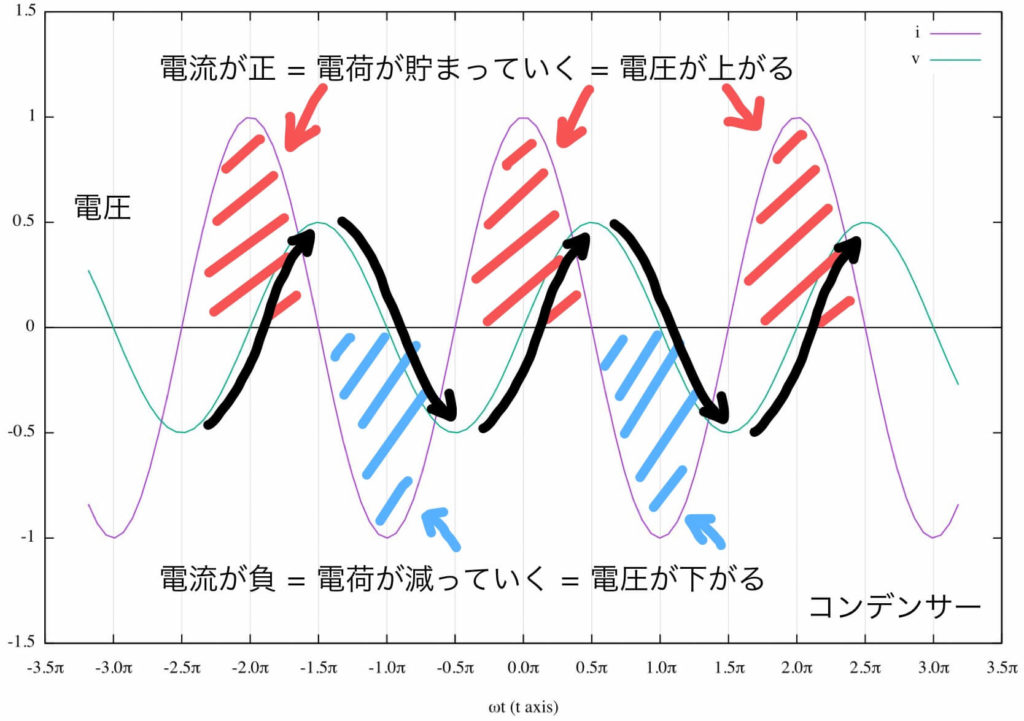
山の位置に注目してグラフを見てみると、
- コンデンサーでは電圧の位相が\( \frac{\pi}{2} \)遅れる
ことがわかるだろう。
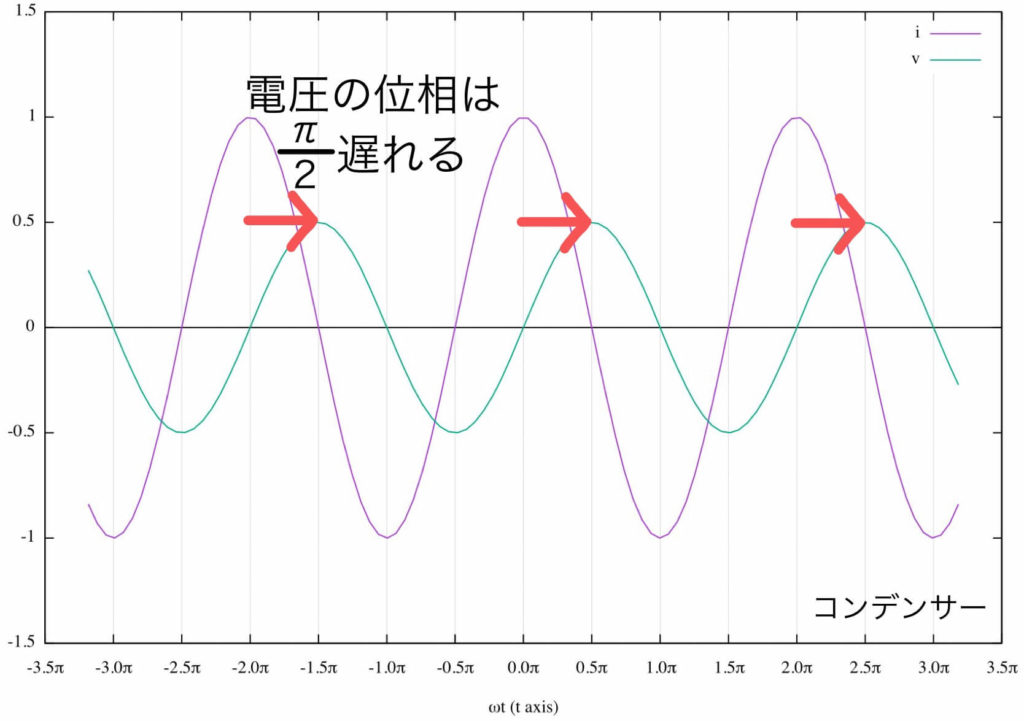
これはコンデンサーが必ず満たしている関係だね。
コンデンサーがどんな回路に接続されていても、コンデンサーに流れ込む電流とコンデンサー部分の電圧はいつもこの関係が成り立っているよ!
コイルで電圧の位相が\( \frac{\pi}{2} \)進む理由
次に自己インダクタンスが\( L \)のコイルに交流電圧\( v=V_{0}\sin{\omega t} \)がかかったときに、どのような電流が流れるのか考えてみる。

コイルでは、自己誘導として次の式が成り立つことを思い出そう。
\[ v=L\frac{di}{dt} \]
簡単に言うと、流れる電流\( i \)が増減するのに伴って電圧\( v \)(誘導起電力)が生じるという現象だった。このような単純な場合に限らず、コイルを流れる電流とコイルにかかっている電圧はいつでも必ずこの式を満たしている。
電流が増加しているときは電圧が正(抵抗に電流が流れているときのように電圧降下している状態)であり、電流が減少しているときは電圧が負である。
さらに言っておくと、電流の変化が急(電流のグラフの傾きが急)であればあるほど電圧は大きくなる。
これをグラフにしてみよう。
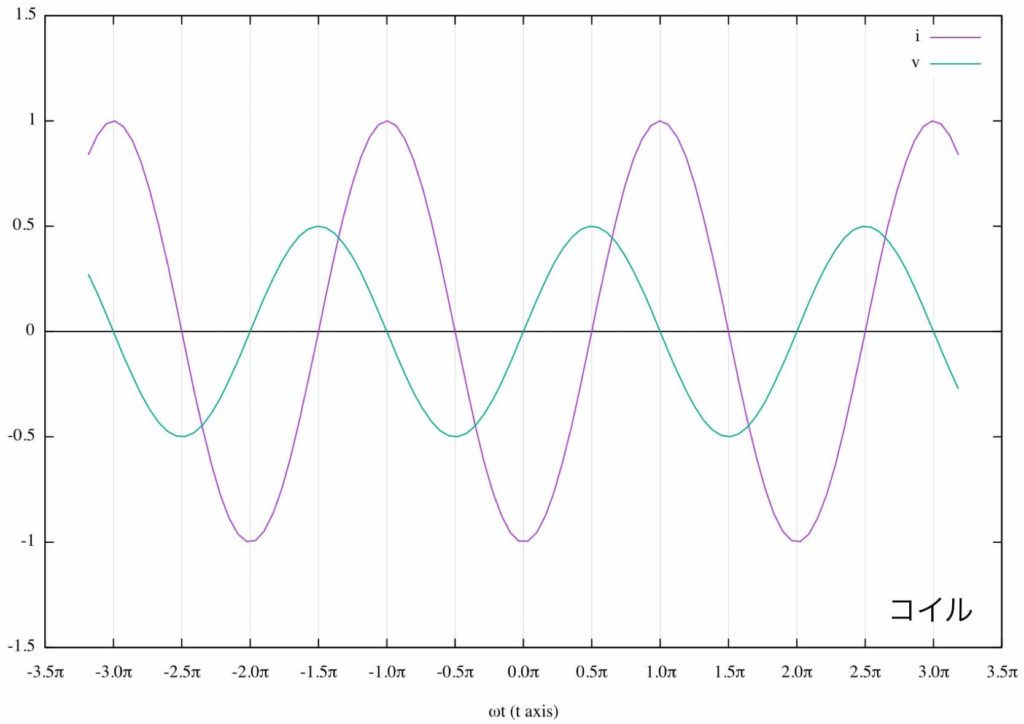

ここでは\( \omega t = 0 \)で電流が\( 0 \)となるようにグラフを描いた。これに説明を加える。
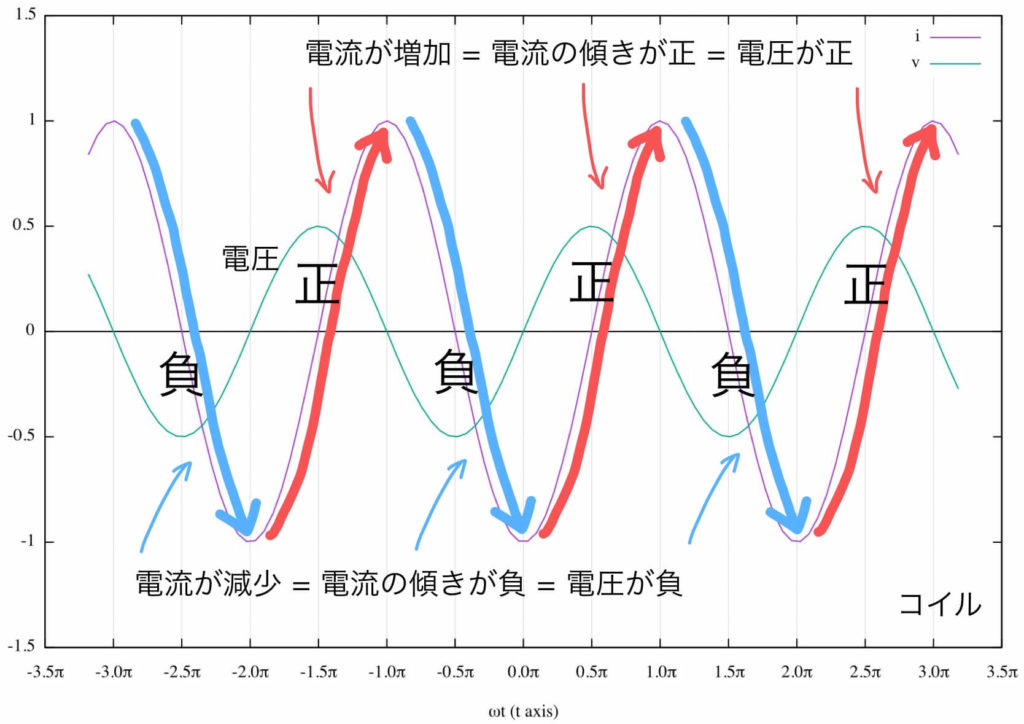

山の位置に注目してグラフを見てみると、
- コイルでは電圧の位相が\( \frac{\pi}{2} \)進む
ことがわかるだろう。
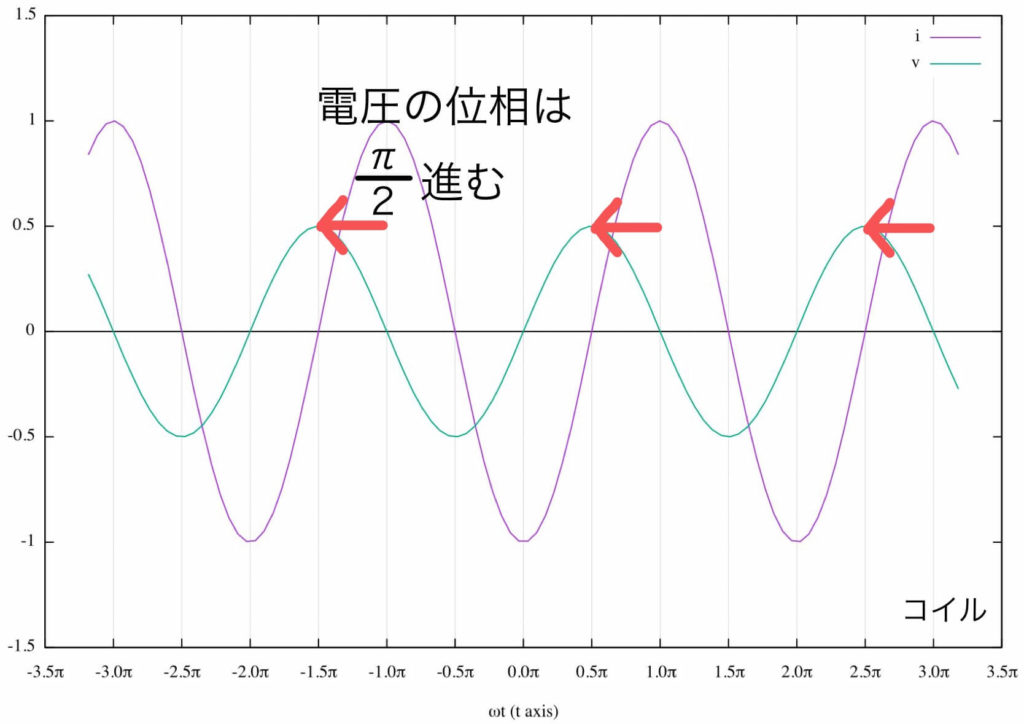



ここまでで、交流回路でコイルやコンデンサーの電圧の位相が進む・遅れると言われる理由がイメージできただろう。
最後に具体的な計算を簡単に見ていくことにする。
電流と電圧の関係(具体的な計算)
必要な数学
コンデンサーやコイルの位相について完全に理解するには、微分(より正確には微分方程式)についての知識が必要だ。
と言っても実はそれほど難しくはない。ここではそのために必要な数学について確認する。
三角関数の微分
\[ \frac{d}{dt}\sin{\omega t} = \omega\cos{\omega t} \]
\[ \frac{d}{dt}\Bigl( – \frac{1}{\omega}\cos{\omega t} \Bigr) = \sin{\omega t} \]
コンデンサーで電圧の位相が\( \frac{\pi}{2} \)遅れる理由
まずはじめに電流が電荷の流れ(単位時間あたりに流れる電荷)だったことを思い出すと、次の式が成り立つ。
\[ i=\frac{dQ}{dt} \]
電流が正となる向きは読者各自で好きに決めて良いが、ここではコンデンサーに電荷が貯まる向きを正としている。
さらにコンデンサーでは次の方程式が成り立っていることは先ほど確認した。
\[ Q=Cv \]
これを時間微分する。
\[ \frac{dQ}{dt}=C\frac{dv}{dt} \]
電流と電圧の関係式から、次のようになる。
\[ i=C\frac{dv}{dt} \]
ここに\( v=V_{0}\sin{\omega t} \)を代入する。
\[ i=\omega CV_{0}\cos{\omega t} \]
これを位相が見やすいように書き換える。
\[ i=\omega CV_{0}\sin{\Bigl( \omega t + \frac{\pi}{2}} \Bigr) \]
位相を見ればわかるように、\( v \)の位相\( \omega t \)が\( i \)の位相\( \omega t + \frac{\pi}{2} \)に追いつくのに\( \frac{\pi}{2\omega} \)だけ時間がかかる。言い換えると、位相が\( \frac{\pi}{2} \)だけ遅れる。
ここで求まった\( i \)と\( v \)を1つのグラフで描いたものが、先ほど見たようなこのグラフである。
- \( v=V_{0}\sin{\omega t} \)
- \( i=\omega CV_{0}\sin{\Bigl( \omega t + \frac{\pi}{2}} \Bigr) \)




コイルで電圧の位相が\( \frac{\pi}{2} \)進む理由
次にコイルについて見ていこう。
コイルでは以下の関係式が成り立っていた。
\[ v=L\frac{di}{dt} \]
ここに\( v=V_{0}\sin{\omega t} \)を代入する。
\[ V_{0}\sin{\omega t}=L\frac{di}{dt} \]
解きやすいようにこの式を書き換える。
\[ \frac{di}{dt}=\frac{V_{0}}{L}\sin{\omega t} \]
先ほど確かめたように\( \frac{d}{dt}\Bigl( – \frac{1}{\omega}\cos{\omega t} \Bigr) = \sin{\omega t} \)だったので、\( i \)は次のように求まる。
\[ i = -\frac{V_{0}}{\omega L}\cos{\omega t} \]
これを位相が見やすいように書き換える。
\[ i = \frac{V_{0}}{\omega L}\sin{\Bigl( \omega t – \frac{\pi}{2}} \Bigr) \]
位相を見ればわかるように、\( v \)の位相\( \omega t \)は\( i \)の位相\( \omega t – \frac{\pi}{2} \)より\( \frac{\pi}{2\omega} \)だけ時間が早く進んでいる。言い換えると、位相が\( \frac{\pi}{2} \)だけ進む。
ここで求まった\( i \)と\( v \)を1つのグラフで描いたものが、先ほど見たようなこのグラフである。
- \( v=V_{0}\sin{\omega t} \)
- \( i=\frac{V_{0}}{\omega L}\sin{\Bigl( \omega t – \frac{\pi}{2}} \Bigr) \)




電流と電圧の関係(まとめ)
コンデンサー
電圧
\( v=V_{0}\sin{\omega t} \)(こう仮定する)
電流
\( i=\omega CV_{0}\sin{\Bigl( \omega t + \frac{\pi}{2} \Bigr)} \)
電流の位相に比べて、電圧の位相は\( \frac{\pi}{2} \)遅れている
電圧の位相:\( \omega t \)
電流の位相:\( \omega t + \frac{\pi}{2} \)




コイル
電圧
\( v=V_{0}\sin{\omega t} \)(こう仮定する)
電流
\( i=\frac{V_{0}}{\omega L}\sin{\Bigl( \omega t – \frac{\pi}{2} \Bigr)} \)
電流の位相に比べて、電圧の位相は\( \frac{\pi}{2} \)進んでいる
電圧の位相:\( \omega t \)
電流の位相:\( \omega t – \frac{\pi}{2} \)




コンデンサーやコイルを見たときはその部分だけに注目して、電流と電圧の関係が決まっていることを思い出すとわかりやすくなることが多いよ!
高校物理の家庭教師


最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!