どうも、かきのたねです。
昨日はセンター試験でしたね。今回は2019年度のセンター物理をわかりやすく解説していきます。
次は第3問。





問1:薄膜の干渉

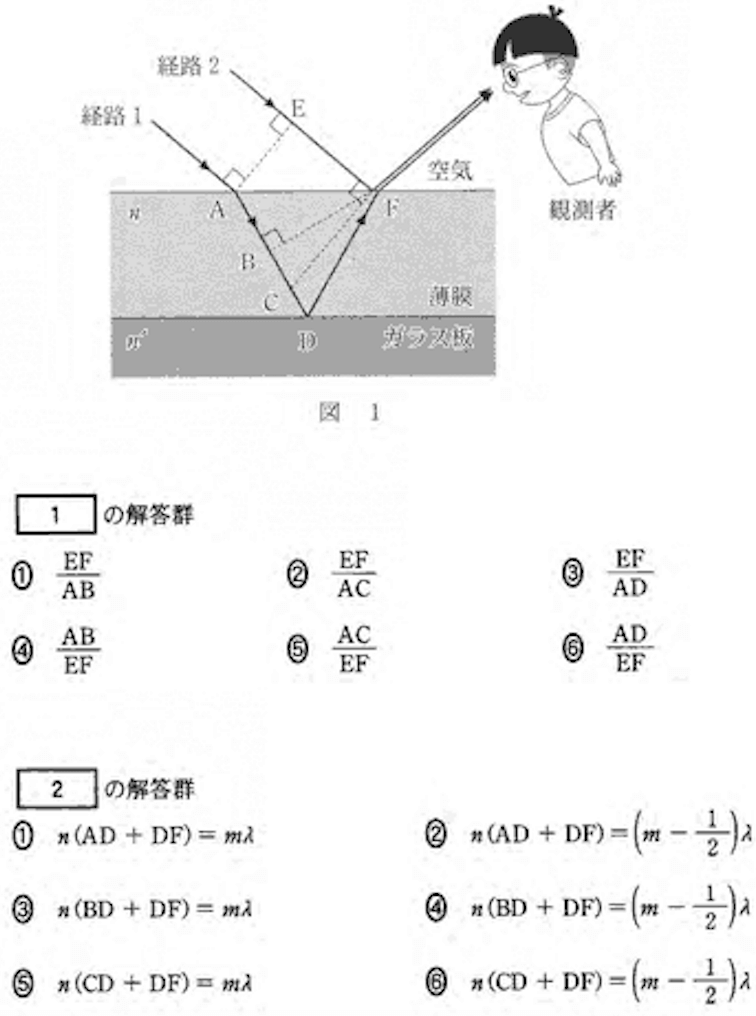
1. 屈折の法則(スネルの法則) 答:1
【公式】スネルの法則
屈折率\( n_{1} \)の媒質から屈折率\( n_{2} \)の媒質へと屈折するとき、次の関係が成り立つ。
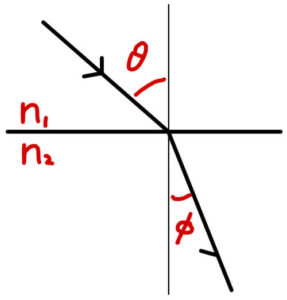
今回使うのはこれだけだが、他にこれらの関係も成り立つ。
\( \lambda \):波長
\( v \):媒質中の速さ
この問題の場合、空気の屈折率が1なので次のようになる。
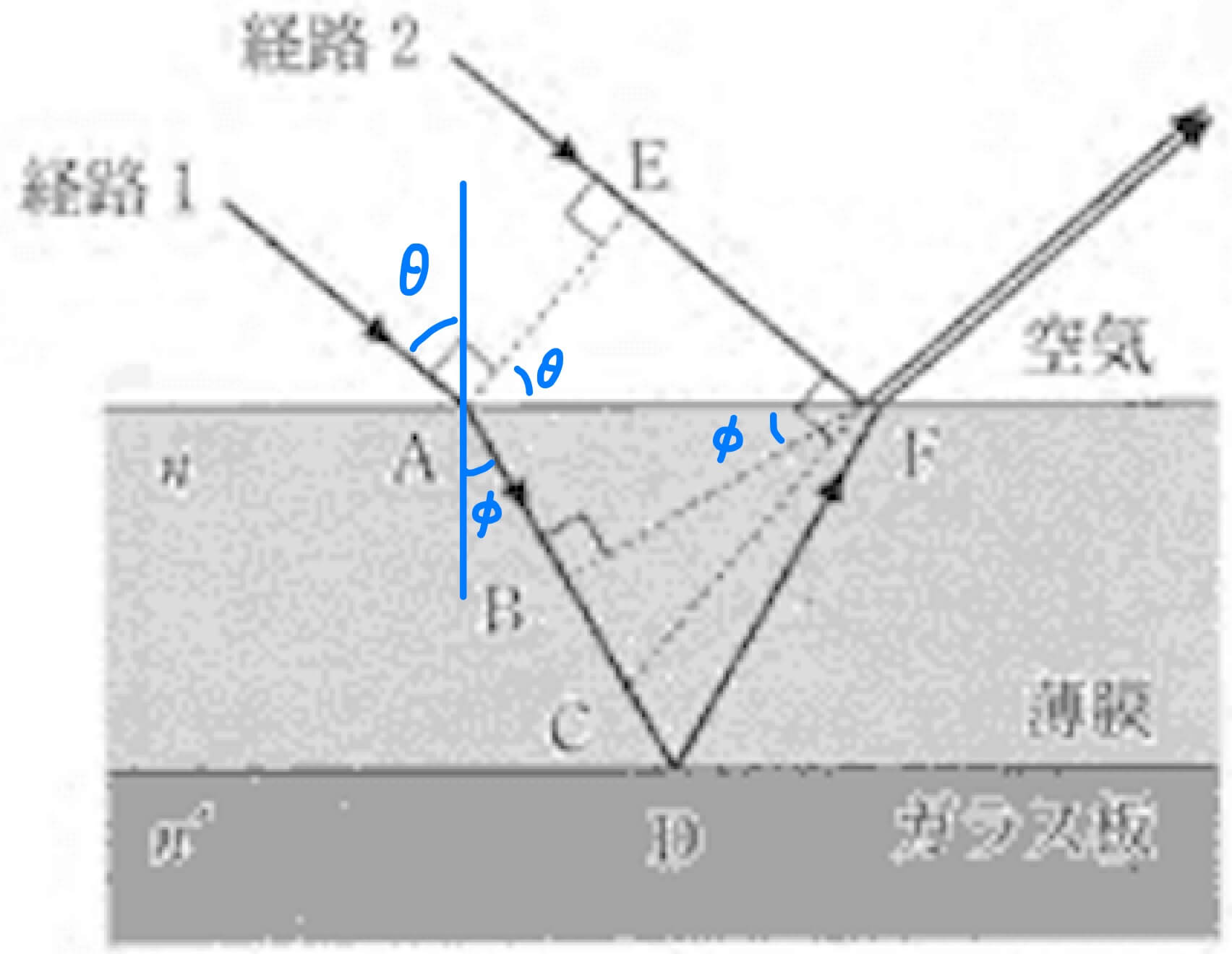
図から\( \sin{\theta } \)と\( \sin{\phi } \)の大きさを求められる。
これより\( n \)は、
これは1
2. 強めあいの条件 答:3
【公式】干渉条件
同位相で出た波が途中で位相変化しない場合、
強めあいの条件:同位相
弱めあいの条件:逆位相
【公式】光路差
屈折率\( n \)の媒質中を光が進むとき、この光は空気中に進む距離の\( \frac{1}{n} \)倍と短くなる。
空気中を進む光と媒質中を進む光の経路差を計算する場合、媒質中での経路は\( n \)倍する。
このようにして計算したものを\( 光路差 \)という。
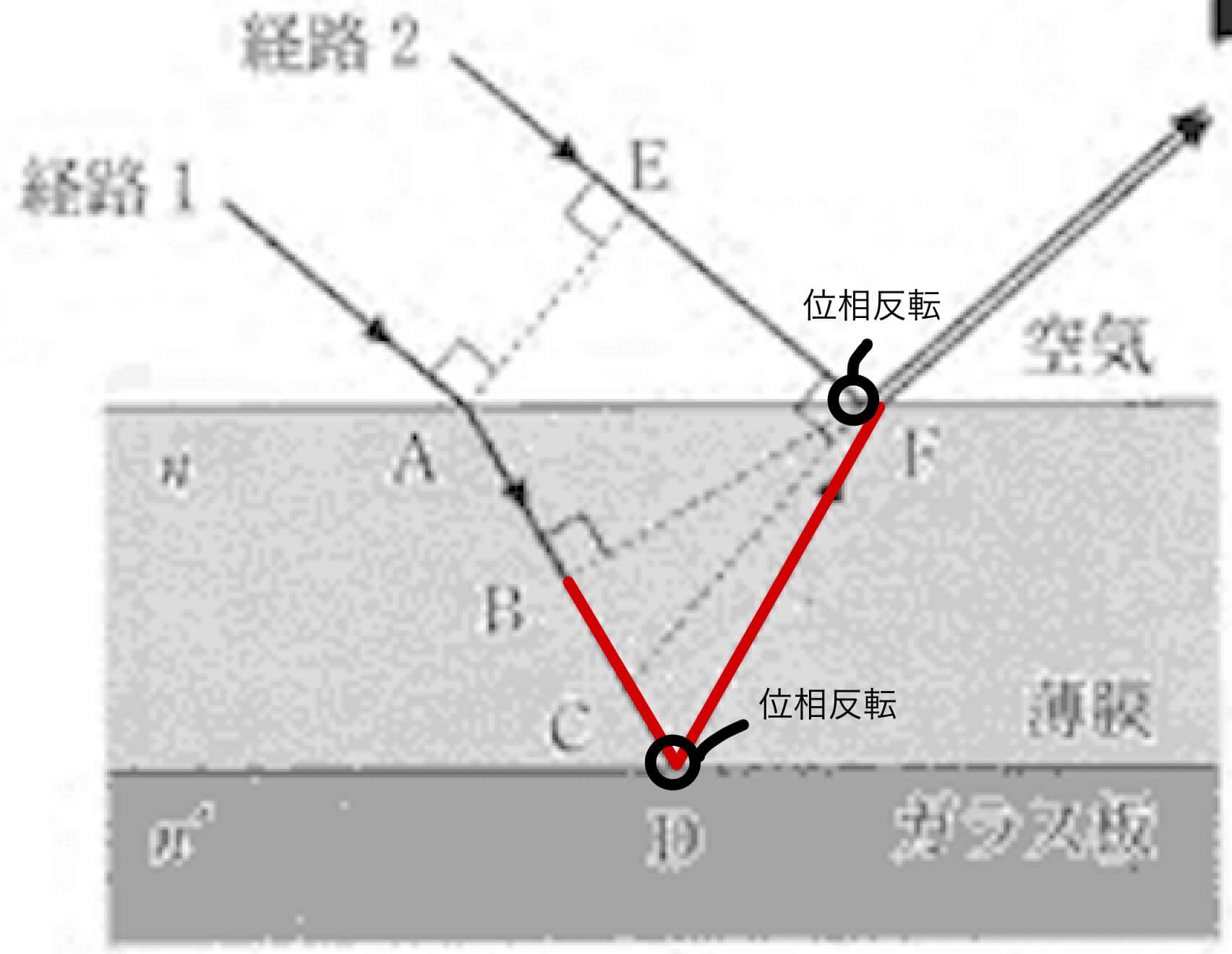
経路1と経路2の光路差は\( n(AB + BD + DF) – EF \)であるが、\( nAB = EF \)なので
屈折率が小さい媒質から大きい媒質に向かって反射するとき、固定端反射して位相が反転する(位相が\( \pi \)ずれる)。
今回は経路1でも経路2でも反射の際に位相が反転する。結局強めあいの条件は、
(光路差)=(波長の整数倍)
よって
答えは3
問2:光の屈折 答:4,2
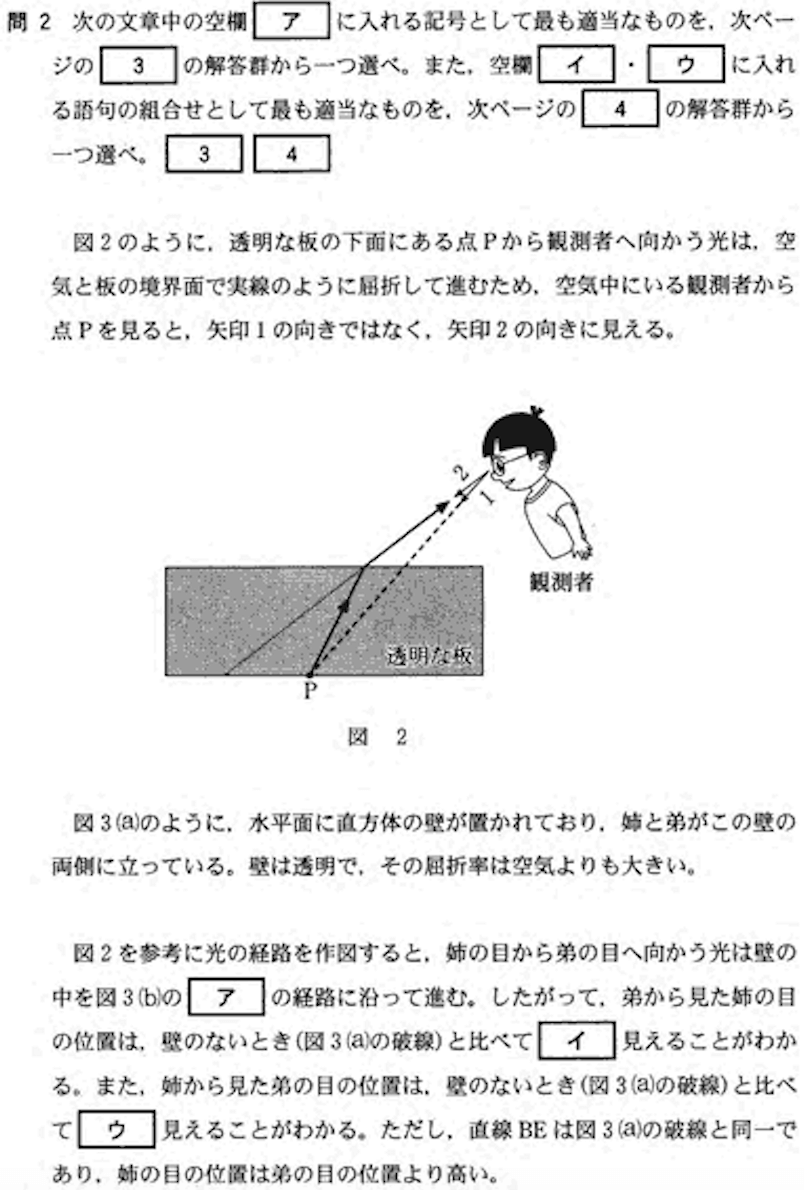
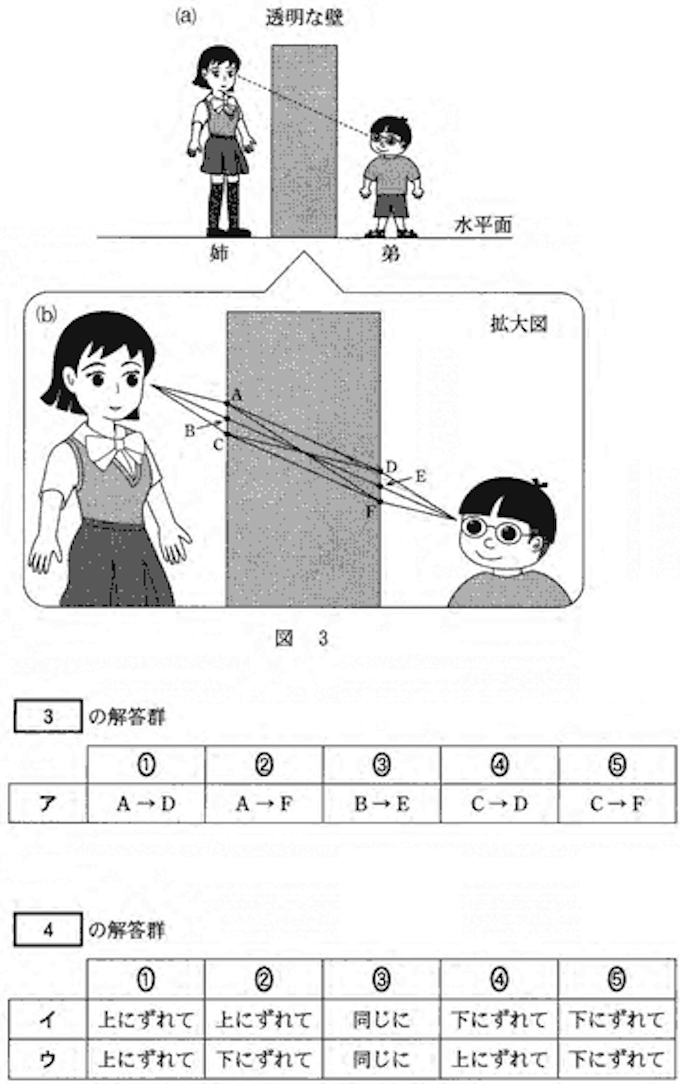
先ほど用いたスネルの法則をもう一度使う。
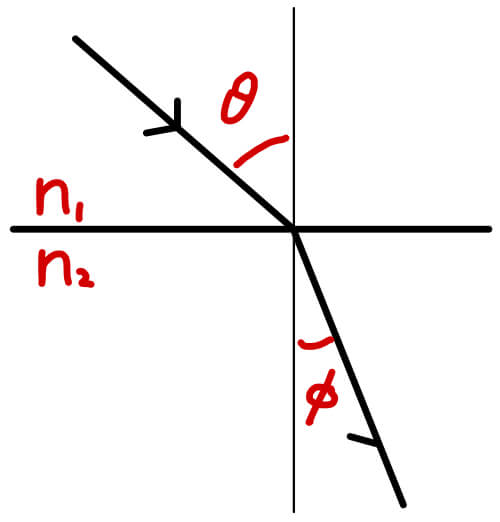
この式からわかるように\( n_{1} < n_{2} \)なら\( \sin{\theta } > \sin{\phi } \)、つまり\( \theta > \phi \)
屈折率の大きい方が角度は小さく、屈折率の小さい方が角度は大きい。
これを満たすのは4のみ
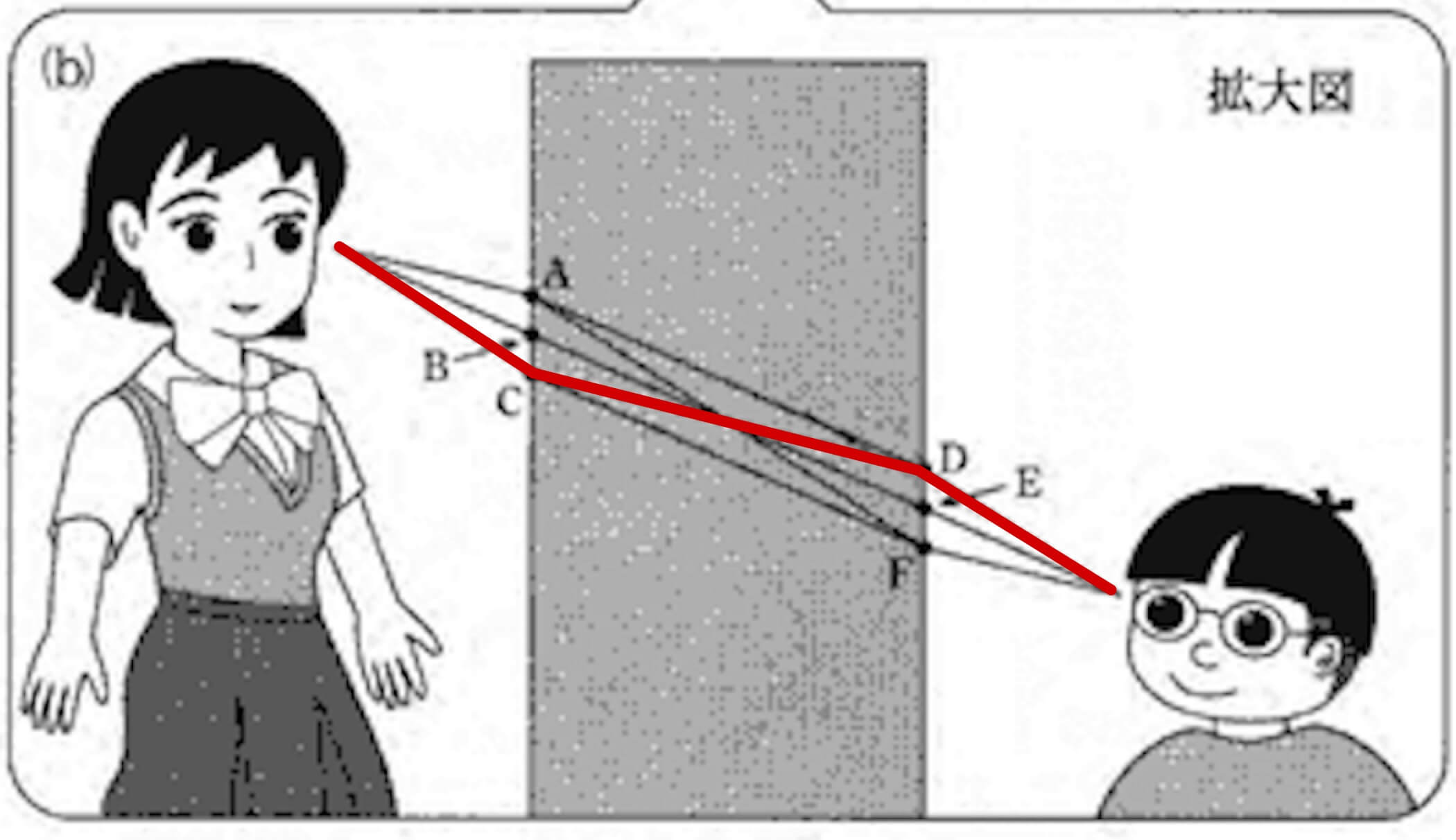
それぞれの目線を図示すると次のようになる。
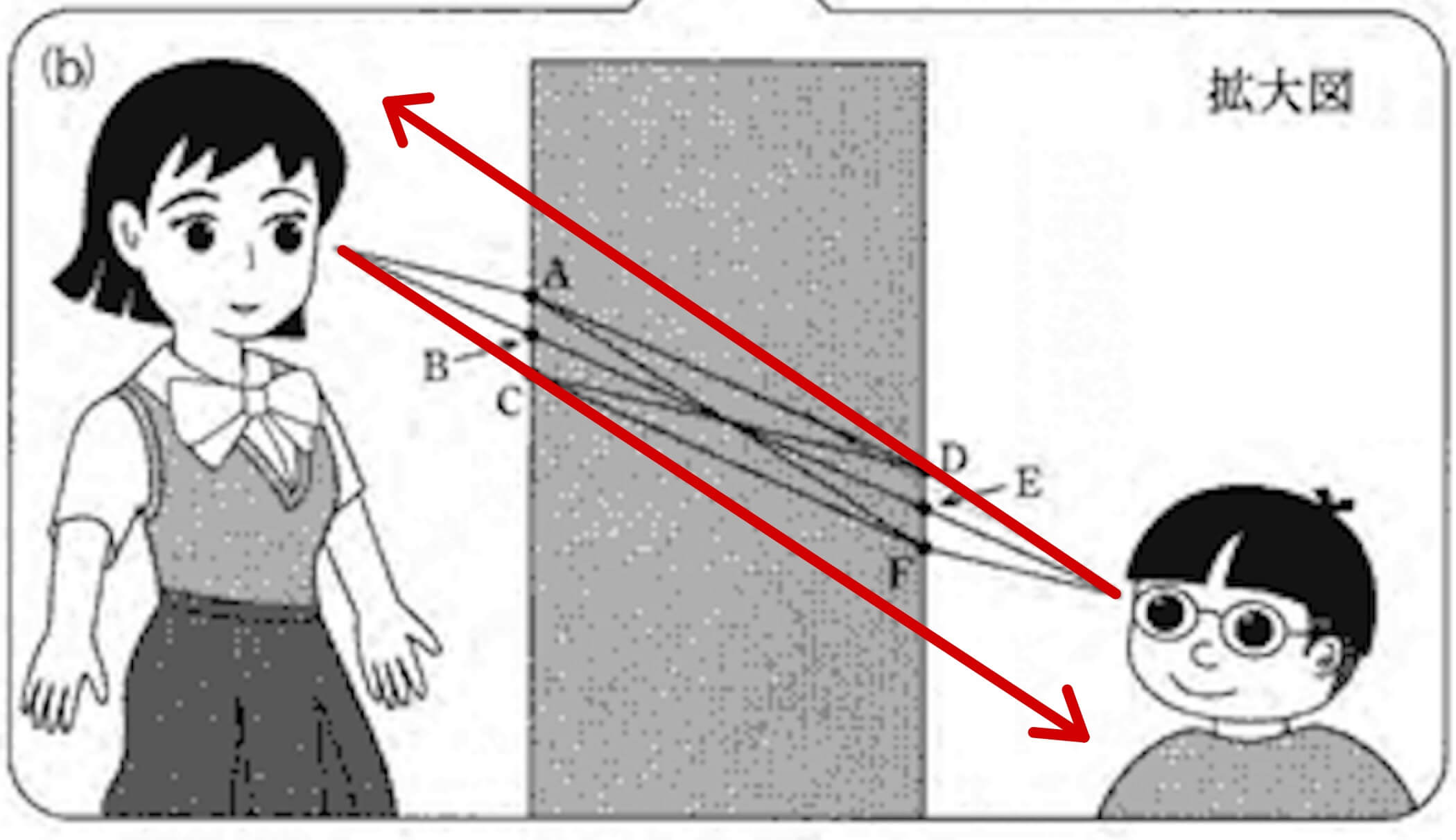
弟から見たとき、姉の目は実際よりも上にずれて見える。
姉から見たとき、弟の目は実際よりも下にずれて見える。
よって答えは2
問3:正弦波 答:4



グラフを見ると\( x = a \sin{\frac{2\pi t}{T}} \)を半周期分左にずらしたものになっている。
x = a \sin{\frac{2\pi t}{T} + \frac{\pi }{2}}
よって答えは4
次のように、無理やり計算で求めることもできる。
【数学公式】余角の公式, 補角の公式
グラフをそのまま読み取ると
である。これを上の公式を使うと次のように書き換えられる。
よって答えは4
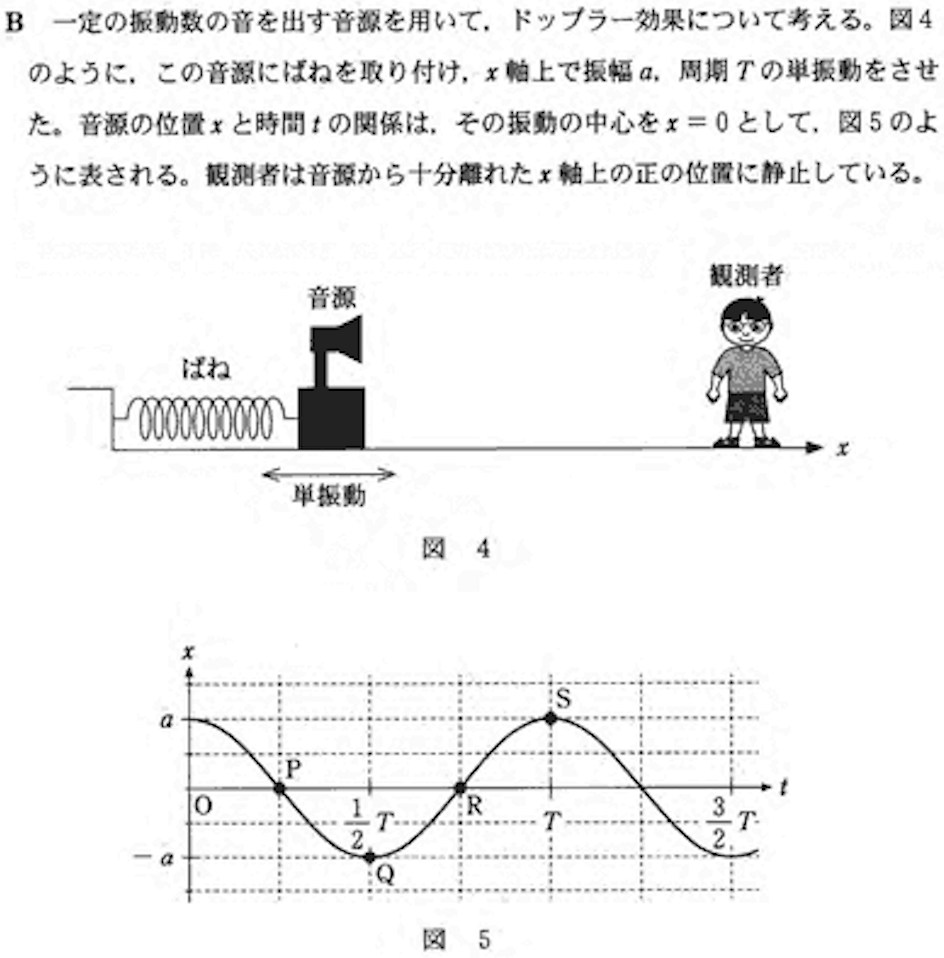
問4:ドップラー効果 答:3


【公式】ドップラー効果の公式


音源が振動数\( f_{0} \)の音(音速\( V \))を出すとする。
音源が動くと波長が変わり、観測者が動くと音速が変わったように感じられる。
音源から観測者に向かう向きを速度の正の向きとすると、観測者が聞く音の振動数\( f’ \)は次のようになる。
「最も高い音」とは、「最も振動数の大きな音」である。
ドップラー効果で振動数が最大なのは波長が最短になっているときで、音源が観測者に向かう速度が最大になるとき。
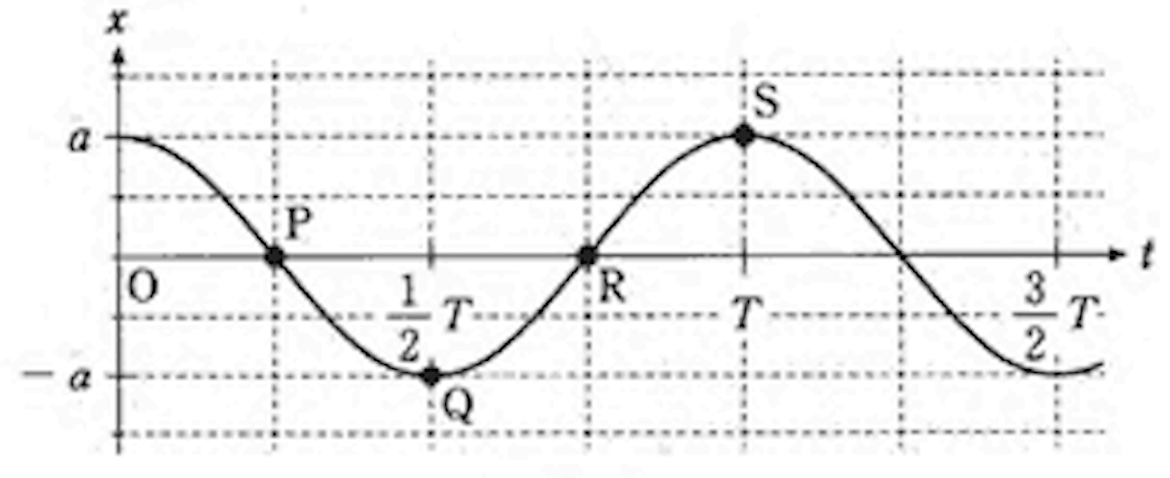

図で\( x \)方向の速度が最大なのは点R
よって答えは3


高校物理の家庭教師


最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!