どうも、かきのたねです。
波の式の求め方って、結構わかり難いですよね。今回は、ある瞬間の波の形(\( yx \)グラフ)、またはある特定の位置での振動(\( yt \)グラフ)が与えられたときの波の式の求め方を解説します。
どちらの場合も波の式の求め方は、次の考えが重要となります。
時刻\( t \),位置\( x \)での変位を求めるのだが、その変位はどこかから伝わってきたものである。
この解説では、波について次の値が与えられているものとします。
- 速さ \( v \)
- 波長 \( \lambda \)
- 振動数 \( f \) (周期 \( T=\frac{1}{f} \) )
- 振幅 \( A \)
問題を解く際は、\( v=f\lambda \) などを使って、予め求めておきましょう。
ある時刻での波の形(\( yx \)グラフ)が与えられているとき
与えられた条件:写真パターン
時刻\( t \)での波が図のようになっていたとしよう。\( x \)は位置、\( y \)は変位を表している。
\[ y = A\sin{2\pi \frac{x}{\lambda }} \]
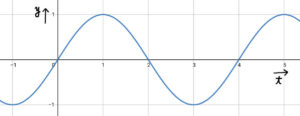
時刻\( t=0 \)で海の波の写真を撮ったようなものだ。
時間経過で波は下のように伝わっていく。この波の式が、今求めたいものである。(ここでは波が右向きに進むこととした)
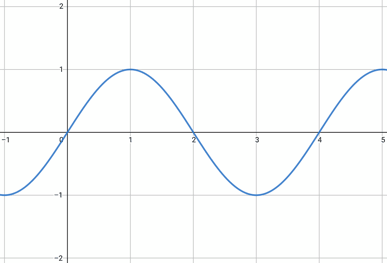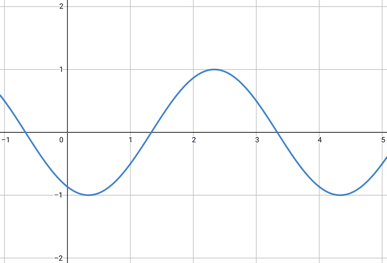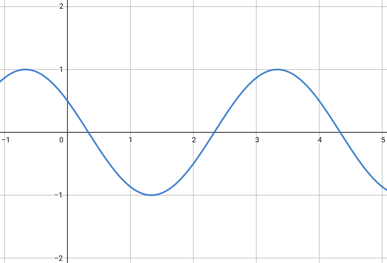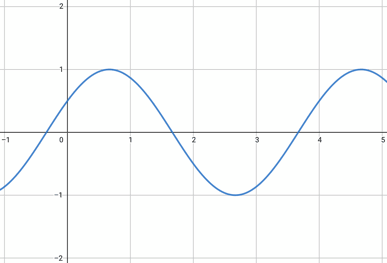

波の式を求める
時刻\( t=0 \)での波は次の式で表せていた。
\[ y(t=0,x) = A\sin{2\pi\frac{x}{\lambda }} \]
波は\( t \)秒間で\( vt \)だけ右向きに進むので、
次の2つの変位は同じである!
- 時刻 \( 0 \), 位置 \( x-vt \)
- 時刻 \(t \), 位置 \( x \)
このことから、
波の式
さらに\( v=f\lambda \)を使うと、次のように書き換えられる。
\[ y(t,x) = A\sin{2\pi (\frac{x}{\lambda }-ft)} \]
これが求めたかった波の式だ。
長さ1mのなかに波が何波長分入っているかを表すものとして、波数\( k \)というものがあるよ。
\[ 波数 : k = \frac{1}{\lambda } \]
これを使うと波の式は、こんな感じに綺麗に書き換えられるんだ。
\[ y(t,x) = A \sin{2\pi (kx – ft)}\]
上の解説では波が右向きに進んでいるものとした。
波が左向きに進んでいるときは、波は\( t \)秒間に\( vt \)だけ左向きに進むので、次の2つの変位が同じとなる。
- 時刻 \( 0 \), 位置 \( x+vt \)
- 時刻 \(t \), 位置 \( x \)
このことから、波の式はこのように変わる。
\[ y(t,x) = A\sin{\frac{2\pi }{\lambda }(x+vt)}\]
ある位置での振動(\( yt \)グラフ)が与えられているとき
与えられた条件:葉っぱパターン
位置\( x=0 \)での媒質の振動が下図のように与えられたとしよう。
\[ y = A\sin{2\pi ft} \]



これはある特定の位置(\( x=0 \))で媒質がどのように振動するのかを表している。その位置で媒質は下のように動く。


海に葉っぱが浮かんでいるようなものだ。
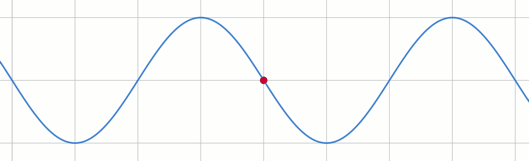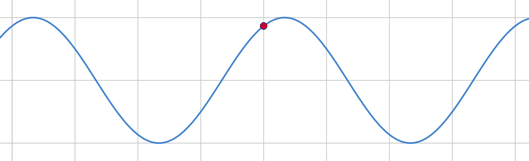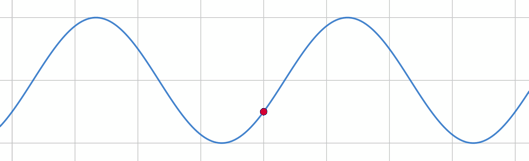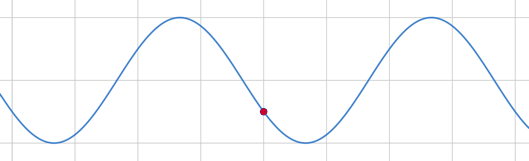
海全体を見ると、波はこのようになっている。この波の式が、今求めたいものである。

波の式を求める
位置\( x=0 \)での振動は次の式で表せていた。
\[ y(t,x=0) = A\sin{2\pi ft} \]
波が右向きに\( x \)だけ進むのに\( \frac{x}{v} \)秒かかるので
次の2つの変位は同じである!
- 時刻 \( t-\frac{x}{v} \), 位置 \( 0 \)
- 時刻 \(t \), 位置 \( x \)
このことから、
波の式
\[ y(t,x) = y(t-\frac{x}{v},x=0) = A\sin{2\pi f(t-\frac{x}{v})} \]
これが求めたかった波の式だ。
このパターンの問題でも波数\( k = \frac{1}{\lambda } \)を使うと、波の式をこのように綺麗に書き直せるよ。
\[ y(t,x) = A\sin{2\pi (ft-kx)} \]
上の解説では波が右向きに進んでいるものとした。
波が左向きに進んでいるときは、波は左向きに速さ\( v \)で原点に向かっていく(\( x>0\)のとき)。位置\( x\)の波が原点まで進むのに\( \frac{t}{v} \)秒かかるので、次の2つの変位が同じとなる。
- 時刻 \( t+\frac{x}{v} \), 位置 \( 0 \)
- 時刻 \(t \), 位置 \( x \)
このことから、波の式はこのように変わる。
\[ y(t,x) =A\sin{2\pi f(t+\frac{x}{v})} \]
まとめ
右向きに進む波の式
写真パターン:\( yx \)グラフ\( y=y(t=0,x) \)から求める
\[ y(t,x) = y(t=0,x-vt) \]
葉っぱパターン:\( yt \)グラフ\( y=y(t,x=0) \)から求める
\[ y(t,x) = y(t-\frac{x}{v},x=0) \]
左向きに進む波の式
写真パターン:\( yx \)グラフ\( y=y(t=0,x) \)から求める
\[ y(t,x) = y(t=0,x+vt) \]
葉っぱパターン:\( yt \)グラフ\( y=y(t,x=0) \)から求める
\[ y(t,x) = y(t+\frac{x}{v},x=0) \]
高校物理の家庭教師


最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!