どうも、かきのたねです。
今回は、物理で高得点を取っている人が必ずやっていることを紹介します。これを知っていれば計算ミスを防ぐだけでなく、計算ミスをしてしまっても瞬時に発見できるようになります。
単位チェック
物理に出てくる値には必ず単位が付いている。例えば速度vには v[m/s] が付いているし、質量mには m[kg] が付いている。
異なる単位を持つ数は足し引きできない。速度と質量を足しても無意味であるということだ。逆に単位が異なる数を足し引きしている場合(例えば v+m )、どこかで必ず計算を間違えている。
計算式の単位を確認しておかしな計算がないかどうか、いつもチェックするクセをつけておこう!
計算結果自体の単位を確認することも大切だ。速さを求めているのに答えが mv[kg・m/s] となっていてはいけない。最初のうちは暗算ができるものだけでよいので、求めたい値の単位と計算結果の単位が違っていないか確かめるようにしよう!
ふるまいチェック
こちらも計算結果の確認である。端的に言ってしまえば、極端な状況を考えるというものだ。これは例を見るとわかりやすい。
例題1 : 単振動

バネ定数 k のバネに、質量 m の物体がくっついて単振動している状況を考えよう。この振動の周期は次のうちどちらか。必ずどちらかが答えなので、計算はしなくてよい。
\[ (1) \ T = 2\pi \sqrt{ \frac{k}{m} } \]
\[ (2) \ T = 2\pi \sqrt{ \frac{m}{k} } \]
答えは(2)だ。選ぶのにどれくらいの時間がかかっただろうか。公式を使わずとも30秒以内には答えて欲しい問題だ。
なぜ(2)だと瞬時に判断できるのか。例えば質量 m がとても大きな物体であったと考えよう。mが大きくなると、(1)は周期が短くなり、(2)は周期が長くなる。重たい物体は動かしにくく、周期は長くなるはずなので(2)だとわかるのだ。
もう1つの考え方としてバネ定数 k が大きい、つまりバネが硬い状況を考えてみよう。このときバネが物体を引く力が大きくなるので、それだけ速度が早く変化し、周期は短くなるはずだ。kを大きくすると周期 T が大きくなるのは(2)なので、これが答えとなる。
例題2 : 衝突
もう1つの例題を見てみよう。
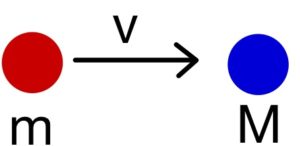
質量 M で静止している物体に、質量 m の物体が速さ v で弾性衝突する場合を考える。この時衝突後の質量 M の物体の速さ V はいくらか。

\[ (1) \ V = \frac{2mv}{M+m} \]
\[ (2) \ V = \frac{2mv}{M-m} \]
これは一瞬で答えられないといけない。答えは(1)だ。
ここでのふるまいチェックは、両方の質量が同じだった場合を考えれば良い。これは同じ物体がただ弾性衝突するだけだ。しかし(2)の分母は M-m なので、Vが無限大に発散してしまう。これはおかしい。(2)ではないのは明らかなのだ。
ふるまいチェックとは
上の2つの例で言いたかったのは、極端な例を考えてみておかしなことが起こらないか確認してほしいということだ。おかしな事が起こっていれば、その計算結果はほぼ確実に間違っている。
まとめ
単位チェック
- 単位の異なる値を足し引きしていないか
- 計算結果の単位は合っているか
ふるまいチェック
- 特定の場合を考えたときに、おかしなふるまいはしないか
これらを確認する事で、計算を間違えてしまったときにすぐ間違いを発見できるようになる!
高校物理の家庭教師

最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!