どうも、かきのたねです。
前回は、同心円筒形コンデンサーについて解説しました。

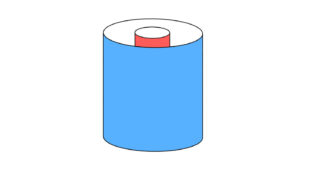
今回は、同心球形コンデンサーの電気容量の求め方を解説します。このようなコンデンサーはあまり見慣れていないものだと思いますが、やり方は前回までと全く同じで簡単です。
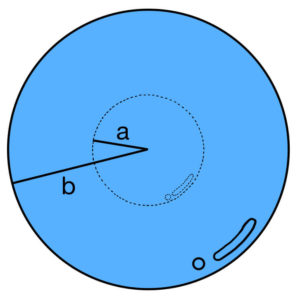
では、どのように電気容量を求めるのか見ていきましょう。
この解説では以下の積分を用います。
電気容量の求め方
Step1
蓄えられた電気量\( Q \)を使って、極板間の電場を求める。
Step2
求めた電場から、極板間の電位差\( V \)を求める。
Step3
電気容量の定義\( C = \frac{Q}{V} \)を使って、コンデンサーの電気容量\( C \)を求める。
同心球形コンデンサー
2枚の球形極板間の電場
まずは中心からの距離が\( r \)の位置での電場の大きさ\( E(r) \)を求めてみよう。
蓄えられている電気量が\( Q \) であるとき、正に帯電した極板からは\( \frac{Q}{\epsilon_{0}} \)本の電気力線が湧き出し、負に帯電した極板には\( \frac{Q}{\epsilon_{0}} \)本の電気力線が流入する。
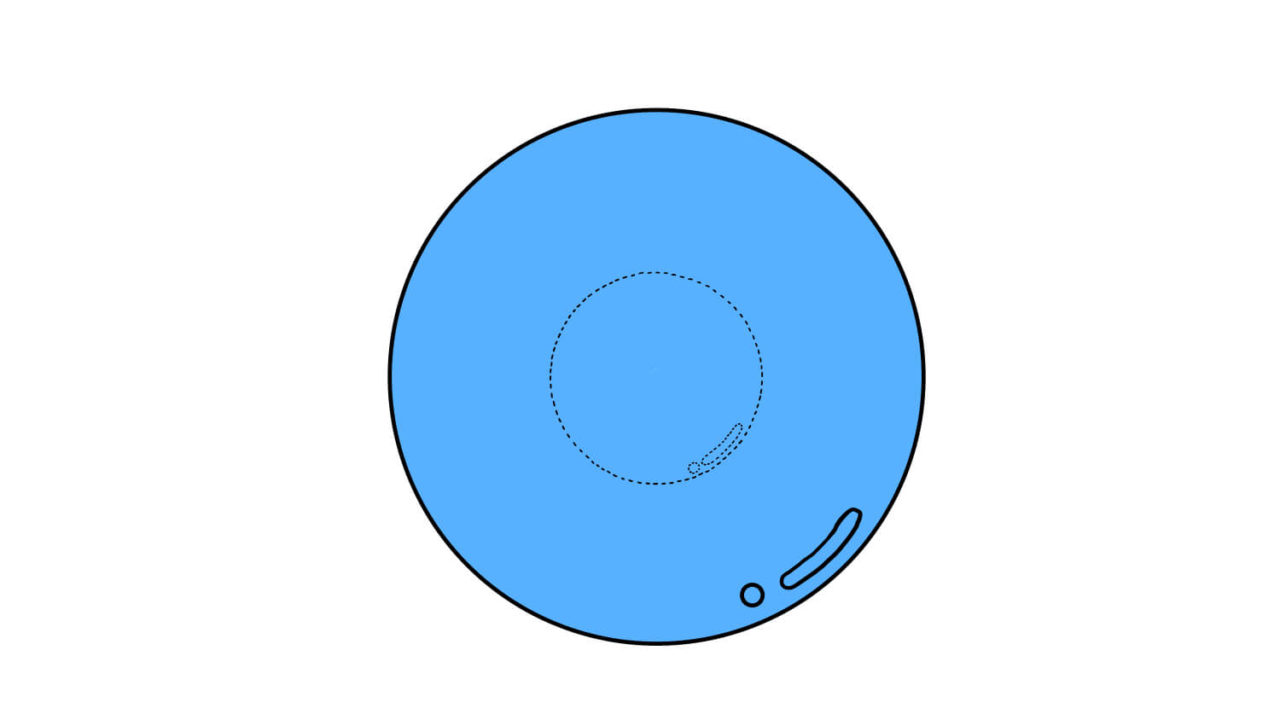
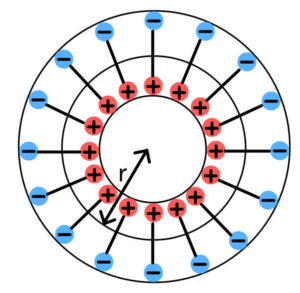
このコンデンサー内部の電気力線の分布を見てみよう。絵を立体的に描くのは難しいので、球の中心を通る断面を下に描いた。
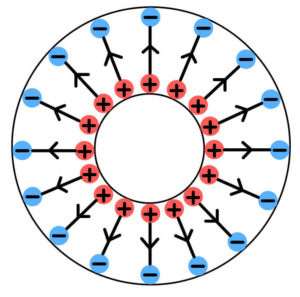
内側の球の半径を\( r=a \)、外側の球の半径を\( r=b \)とする。球形金属内は電気力線が存在できない(金属内の電場は必ずゼロ)ので電気力線は極板間のみに存在し、\( N=\frac{Q}{\epsilon_{0}} \)本が等方的に分布している。
電場の大きさは電気力線の密度であったので、中心から離れれば離れるほど電場は弱くなる。
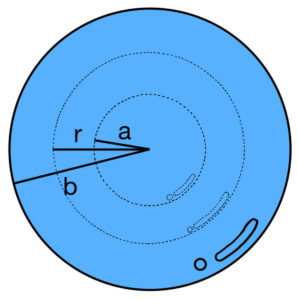
具体的に計算してみよう。半径\( r \)の球の表面積は\( S(r) = 4\pi r^{2} \)なので、この表面を垂直に貫く電気力線の密度\( E(r) \)はこのようになる。
この式を見てわかる通り、電場の大きさは中心軸からの距離の2乗に反比例している。
2枚の球形極板間の電位差
電場が求まったので極板間の電位差も求まる。しかし電場の大きさが中心からの距離に依存しているため、積分計算が必要となる。中心からの距離\( r=a \)の極板と、\( r=b \)の極板との電位差\( V \)は次のように計算できる。
同心球形コンデンサーの電気容量
これで\( Q \)と\( V \)の関係がわかったので、電気容量\( C \)が求められる。
まとめ
- 電気量\( Q \)が蓄えられた同心球形コンデンサーの極板間の電場の大きさ(中心からの距離\( r \))
- 極板間の電位差は
- 電気容量
高校物理の家庭教師

最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!