どうも、かきのたねです。
私達が普段感じている気圧は、ミクロな視点で見るとたくさんの小さな気体分子が肌に当たり、その衝撃を圧力として感じることによっています。このように気体の分子の動きを見るくらいミクロな視点に立った時、普段感じているものがどのような由来なのかを考える理論を気体の分子運動論と言います。
この記事では体積\( V \)の空間内を質量\( m \)の気体分子\( N \)個が平均速度\( v \)で運動しているとき、圧力\( P \)が
\[ P = \frac{Nmv^{2}}{3V} \]
で書き表わせることについて説明していきます。
1粒の気体分子が1回の衝突で壁に与える衝撃
1辺の長さが\( L \)の立方体(体積\( V=L^{3} \))の中で気体分子が自由にバラバラに運動している状況を考え、その中の1粒の気体分子に注目する。
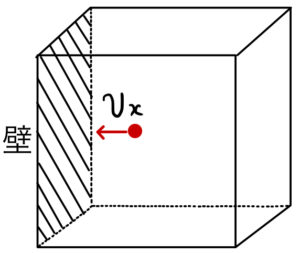
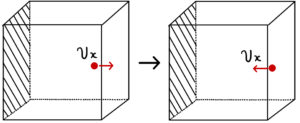
この気体分子が壁に向かってまっすぐぶつかっていくと、弾性衝突をして速さは変わらないまま動く向きが逆になる。
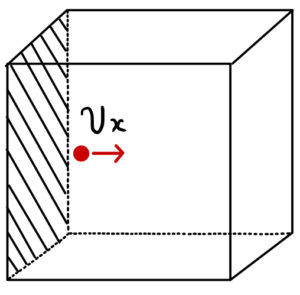
つまり気体分子は壁から反発力を受けるので、壁に近づく向きだった運動量が壁から離れる向きに変化したと言える。
気体分子が壁にぶつかる平均速度を\( v_{x} \)とすると、その気体分子は速度が右向きに\( 2v_{x} \)増えたので、この時の運動量変化は\( 2mv_{x} \)である。
つまり壁は気体分子に\( 2mv_{x} \)の力積を加えて運動量を変化させている。力を加えれば同じ力で押し返されるので(作用反作用の法則)、壁は気体分子から力積\( 2mv_{x} \)を受けたのだ。
N個の気体分子が壁に与える力
1粒の気体分子が1回の衝突で壁に与える力積はわかった。しかし、衝突頻度がわからなければ継続してどれだけの力を与えているのかはわからない。1回の衝撃は同じでも、1秒に1回衝突するのと1分に1回しか衝突しないのとでは、壁が受ける力の平均は大きく異なる。
次はどれくらいの頻度で衝突するのかを計算してみよう。
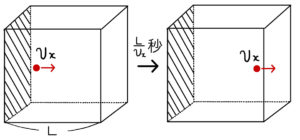
気体分子は壁に衝突した後、速さ\( v_{x} \)で反対側の壁に向かっていく。反対側の壁までの距離は\( L \)なので、\( \frac{L}{v_{x}} \)秒で反対側の壁に衝突する。(こちらの壁も力積を受けているが、今注目している壁ではないのでここでは無視する)
そして反対側の壁ではね返る。
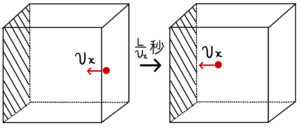
その後同じように速さ\( v_{x} \)で元の壁まで戻っていき、\( \frac{L}{v_{x}} \)秒後に再びこの壁に衝突する。
つまり、1回衝突してから再度衝突するまでに\( \frac{2L}{v_{x}} \)秒かかるのだ。
1粒の気体分子は\( \frac{2L}{v_{x}} \)秒に1回壁に衝突しているので、気体分子全体としては、\( \frac{2L}{v_{x}} \)秒に\( N \)個の気体分子が壁に衝突する。つまりこの壁は、\( \frac{2L}{v_{x}} \)秒間に\( 2mv_{x}N \)だけの力積を受ける。
ところで力積は、力を加えている時間にその力を掛け算したもの
\[ (力積) = (力) \times (時間) \]
なので逆に、与えられた力積を時間で割り算すれば、その時間内で平均してどれだけの力が壁にかかっているかわかる。
\[ (力) = \frac{(力積)}{(時間)} \]
\( \frac{2L}{v_{x}} \)秒間に\( 2Nmv_{x} \)だけの力積が与えられているので、壁には平均して
\[ (力) = \frac{2Nmv_{x}}{\frac{2L}{v_{x}}} = \frac{Nmv_{x}^{2}}{L} \]
だけの力が加わる。
実際は気体分子が衝突した瞬間にだけ力が加わるのだが、気体分子の数は膨大なので、常に気体分子が衝突していると考えて良い。衝突している気体分子の数はいつでも同じなので、壁に加わっている力はそれを平均したものと同じになる。
これで、壁には大きさ\( \frac{Nmv_{x}^{2}}{L} \)の力が加わっているとわかる。
壁にかかる圧力
圧力\( P \)は、かかっている力を面積で割り算すれば求められる。
\[ (圧力) = \frac{(力)}{(面積)} \]
壁の面積は\( L^{2} \)なので、
\[ P = \frac{Nmv_{x}^{2}}{L^{3}} \]
だとわかる。
これで圧力がわかった訳だが、\( v_{x} \)は気体分子が壁にぶつかっていく方向の平均速度だったことを思い出してほしい。方向は他に2方向ある。これを\( y,z \)方向とすると\( v \)と\( v_{x},v_{y},v_{z} \)との関係は、次のようになる。
\[ v^{2} = v_{x}^{2} + v_{y}^{2} + v_{z}^{2} \]
気体分子は空間3方向(\( x,y,z \)方向)バラバラに運動していてどの方向にも偏っていないので、
\[ v_{x}^{2} = v_{y}^{2} = v_{z}^{2} \]
よって、次の関係が導かれる。
\[ v_{x}^{2} = \frac{v^{2}}{3} \]
これを先ほどの圧力の式に入れることで、求めたかった関係式
\[ P = \frac{Nmv^{2}}{3L^{3}} = \frac{Nmv^{2}}{3V} \]
を得ることができた。
高校物理の家庭教師

最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!