どうも、かきのたねです。
相対性理論って、一度は興味を持ったことがあると思います。今日は相対性理論で特に有名な時間の遅れについて、わかりやすく話していこうと思います。
前提とする知識は三平方の定理だけです!!
ずっと気になっていた相対性理論、今ここで理解しちゃいましょう!
アインシュタインの疑問と相対性原理
まずは相対性理論の発見の元となったアイディアを見てみよう。
アインシュタインは次のような疑問を抱いた。
普通に考えるなら、光と同じ速さで走ったら鏡に光が当たらないから顔は見えないはずだ。
自分が遅ければ顔は鏡に映り、自分が速く走れば顔は鏡に映らない。
こう考えるのには理由がある。アインシュタインの時代より2世紀ほど前に、ガリレオ・ガリレイという人は次のような原理を発見していた。
ガリレイの相対性原理
慣性系(静止していたり、速度を変えずに運動している状況)にいる人には、それがどのような慣性系であっても運動の仕方が変わらない。
簡単に言ってしまえば自分が等速で動いていたとしても、物を落とせば真下に落ちていくし、物を投げれば止まっていながら投げた時と同じように飛んでいく。
例えば自分が船の中から、窓を見ている状況を考えてみよう。
窓の先を別の船が横切ったとき、それは自分が通り過ぎたのか相手が通り過ぎたのかわかるだろうか?
どちらが動いていたのかはわからないだろう。
「自分から見ると、(相対的に)相手は動いているな」
ということしかわからないのだ。つまり、どちらが止まっているのかわからない。
どんなに頑張っても、宇宙の基準(宇宙のどこが動いていないのか)を知ることはできないのだ。
これを先ほどのアインシュタインの考えと合わせると、光の進み方で宇宙の基準がわかってしまう事になる。宇宙の基準からの速さで、自分が鏡にどう映るかがわかるはずだから。
「では確かめようじゃないか」となるだろう。ちょうどアインシュタインの考えとは無関係に、そんなことが起こるのかを実験した人たち(マイケルソンとモーリー)がいた。
地球は毎秒30kmという、超高速で太陽の周りを公転していることが知られている。
そのため正面から来る光の速さと、真後ろから来る光の速さは違うはずだ。
この光の速さの違いを検出しようとしたのだが、どう頑張っても違いはほとんど見られなかった。
失敗したのだ。
この実験の失敗は、光のもつ不思議な性質を暗示している。
光速度不変の原理 〜光の不思議な性質〜
相対性理論を理解するのに一番重要なのは、光の性質だ。ここで光のもつ不思議な性質を紹介しよう。
光速度不変の原理
慣性系(静止していたり、速度を変えずに運動している状況)にいる人は、それがどのような慣性系であっても光の速さは常に秒速30万kmである。
「ぼーっと止まっている人にも、車に乗っている人にも、ロケットに乗っている人にも、誰にとっても光は必ず秒速30万kmで進むように見える」ということだ。
不思議すぎる。しかし色々な実験結果を確かめると、こうなっていないといけないようだ。
これは不思議な現象を引き起こす。
時間の遅れ
鏡を持ちながら光を追いかけると何が起こるのか考えてみよう。と言いたいところなのだが、次の記事で紹介するローレンツ収縮という現象が関わってきてしまう。
代わりに少し複雑に見えてしまうが、等速で動く大きな箱の中にいて光が(鏡など使って)上下に動いていくような状況を、次の2通りで考えてみよう。
光速度不変の原理
誰が見ても光の速さは変わらない
Aさん:箱の中にいる人から見た場合
箱の中にいるAさんには、光(赤い点)がただ上下に進んでいるだけだ。
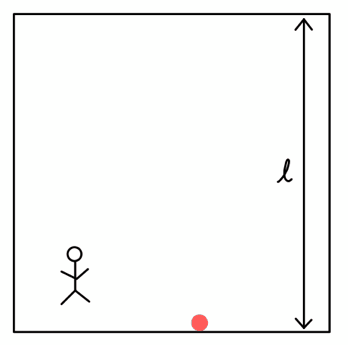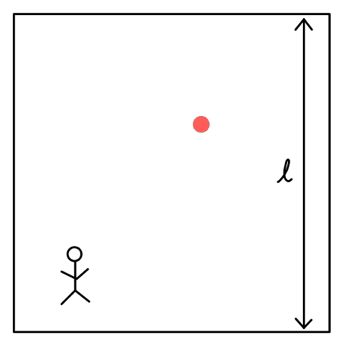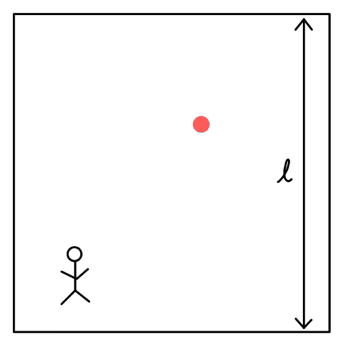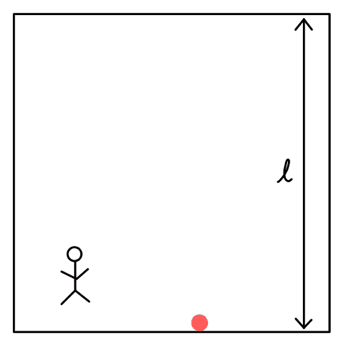

箱の高さを\( l \)とすると、1往復で光は\( 2l \)だけ進む。
そのためAさんには光が\( t_{A}(= \frac{2l}{c}) \)秒間進んでいたように感じられる。(cは光の速さ)
Bさん:箱の外にいる人から見た場合
箱の外にいるBさんには、箱が速さ\( v \)で進んでいるように見えているとしよう。
光が反射して戻ってくるとき、Bさんにはその経路は斜めに見えている。このとき光が進んだ時間を\( t_{B} \)としておく。
普通に考えれば\( t_{A}=t_{B} \)だろう。確かめてみよう。


最初の半分は右斜め上、反射後は右斜め下に進んでいく。それぞれ同じ時間(\( \frac{t_{B}}{2} \))だけかかるので、最初の半分で光が進んだ距離は\( c \frac{t_{B}}{2} \)だ。
その間に箱は\( v \frac{t_{B}}{2} \)だけ進んでいるので、三平方の定理を使うと\( t_{B} \)がわかる。
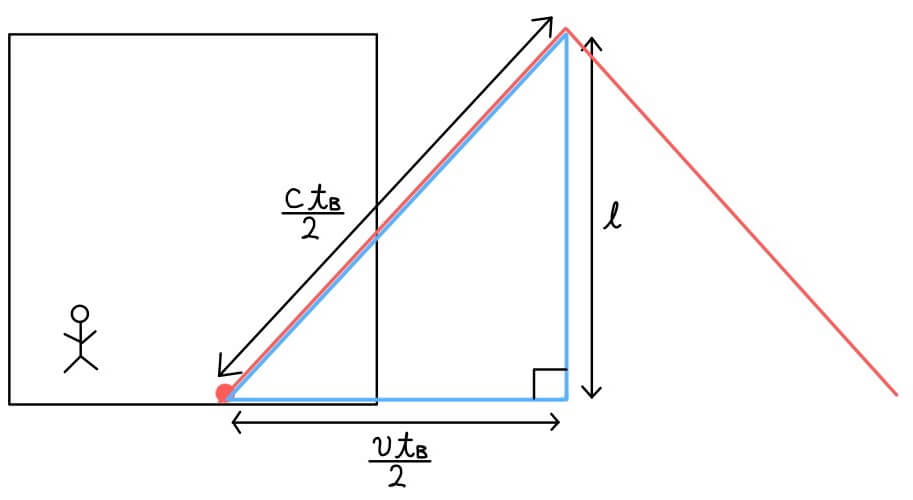

これを\( t_{B} \)について解くと、
観測結果の比較 〜時間の遅れの発生〜
\( t_{A} = \frac{2l}{c} \)だったので、
とわかる。\( \sqrt{1-(\frac{v}{c})^{2}} \leq 1 \)なので、
だとわかったのだ。
これはとても不思議だ。
AさんもBさんも全く同じ現象を見ていたのに、Aさんが測った時間の方が短くなってしまうのだ。
この事実を時間の遅れと解釈する。
速さ\( v \)で走っている人は、体感時間・時計の針が進む時間・ありとあらゆる時間が\( \sqrt{1-(\frac{v}{c})^{2}} (\leq 1) \)倍ゆっくり進んでしまうのである。
ロケットに乗って高速で移動しているだけで、歳をとるのが遅くなっちゃうんだね。
高校物理の家庭教師


最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!