どうも、かきのたねです。
今日は円運動の基礎として知っておきたいものを紹介します。
円運動は単振動のもととなる運動であり、遠心力なども円運動の言葉で説明されます。その基礎を理解しましょう!
円運動とは
円運動とはその名の通り、円軌道を描く運動のことである。
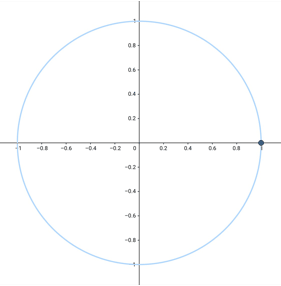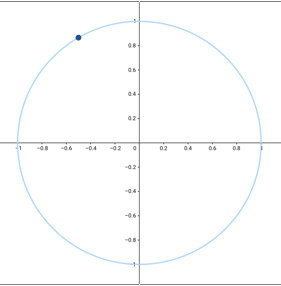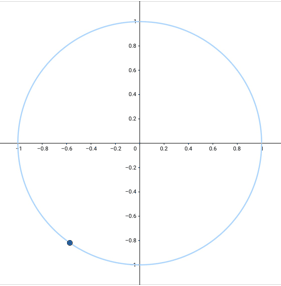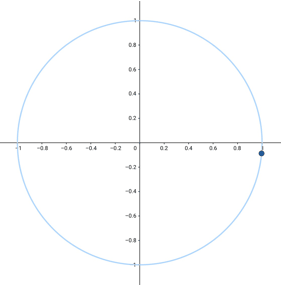
上の動画は等速円運動という、円軌道上を一定の速さで運動する円運動だ。
円運動のポイントは、常に速度が変化していることである。等速円運動は常に一定の速さで動いているが、このとき速度は常に変化している。
速度とは大きさと向きを持つ量(ベクトル)であった。「速さ」と「どの向きに動いていこうとしているのか」の両方の情報を持った量なのだ。
円運動をよく見てみると速さは変わっていなくても、動いていく向きは常に変化しているのがよくわかると思う。
このことに注意すると、遠心力を感じる理由がわかってくる。これは後で説明しよう。
角振動数の導入
円運動といっても、その円の大きさは様々だ。同じ速さで円運動していても、半径が異なれば一周にかかる時間も異なってしまう。
時としてどれだけの角度回転しているのか、回転角の速度はどれくらいかが知りたいときもある。そのため角速度(や角振動数,角周波数)という量を作った。
角振動数はよく\( \omega \)と書かれ、「単位時間[s]あたりにどれくらいの角度[rad]回転するのか」を意味する。回転角の速さだ。
つまり時間\( t \)経過すると、角度\( \omega t \)だけ回転することになる。
この角振動数が同じであれば、どんな半径の円軌道であっても1周にかかる時間は等しい。
円運動の速さと角振動数
円運動の速さも角振動数も同じ運動を見ているので、もちろんそれらは関係している。
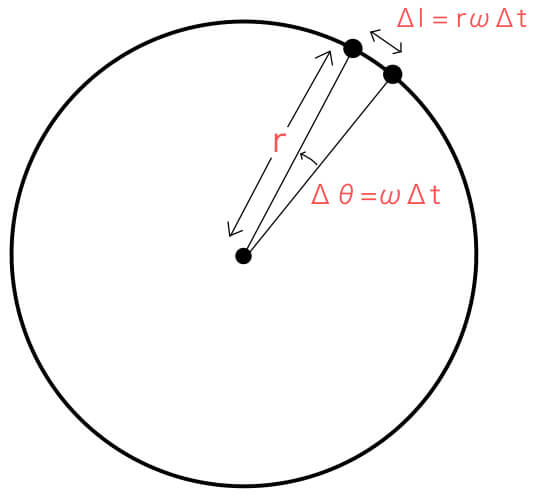
半径\( r \)の円周上をある物体が角振動数\( \omega \)で\( \Delta t \)秒間(一瞬)進んだとしよう。
このとき回転角\( \Delta \theta = \omega \Delta t \)なので、進んだ距離\( \Delta l \)は、次のようになる。
そのため円軌道上を回る時の速さ\( v \)は、
これが円運動の速さと角振動数の関係である。
弧度法
中学校あたりまでは、角度を度数法(\( 30^{\circ},45^{\circ} \)など)で測っていたと思う。
度数法では一周\( 360^{\circ} \) としていた。これは地球が太陽の周りをおよそ360日で1周するため、「一周を\( 360^{\circ} \)としましょう」ということだった。
もっと使いやすい測り方があれば、別の測り方をしてもよいだろう。
ここでは別の測り方である弧度法について話しておこう。実はこの測り方は、度数法よりもわかりやすい定義となっている。
弧度法で測る角度の単位はラジアン(rad)というものを使う。
角度\( \theta \)[rad]とは、「単位円から切り取った長さが\( \theta \)となるような扇型の中心角」である。
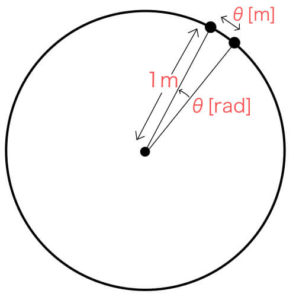
つまり中心角\( \theta \)[rad]で単位円を切り取ると、その扇型の弧の長さは\( \theta \)となる。
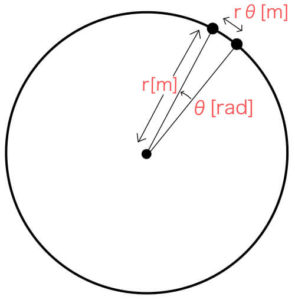
円の半径が\( r \)なら全体が\( r \)倍に拡大され、弧の長さは\( r \theta \)となる。
円運動の加速度
ここでの話は等速円運動に限った話ではないのだが、わかりやすいように等速円運動を例にしながら円運動の加速度を考えていこう。
等速円運動では運動の速さは変わらないが、速度(ベクトル量)は常に円の中心に向かって変化している。
先ほど角振動数\( \omega \)の円運動の速さ\( v=r\omega \)を求めた。次に加速度がどれほどなのかを調べよう。
半径\( r \)の円周上を角振動数\( \omega \)で等速円運動するとき、\( \Delta t \)秒間(一瞬)でどれだけ速度は変化するだろうか?
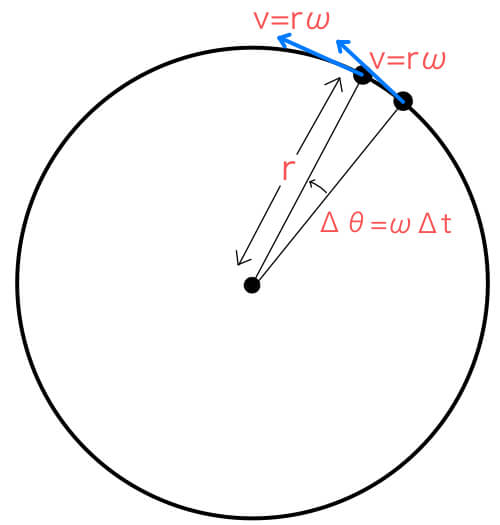
速度は青矢印で表している。この速度(青矢印)の変化量を見るために、青矢印を見やすいように描くとこのようになる。
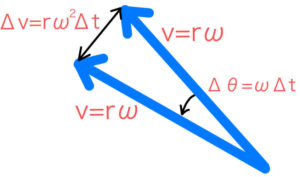
どちらの矢印も長さ\( v \)は\( r\omega \)であり、角度は\( \Delta \theta = \omega \Delta t \)だけ傾いている。
速度(青矢印)の変化量は、それぞれの矢印の先端を結んだ長さなので、
ここから加速度\( a \)が、次のように求まる。
速度は円の中心に向かって変化していくので、この加速度を向心加速度と呼ぶこともある。
円運動をするための条件
ここまでの話面白いのは、円運動の半径\( r \)と角振動数\( \omega \)(もしくは半径\( r \)と速さ\( v \))だけで、中心に向かう加速度がわかってしまうことだ。
円運動をする物体の立場で見たとき、この物体は加速度運動をしているので、慣性力が働いているように見える。この慣性力を遠心力と呼び、中心から離れていこうとしている。この力の大きさ\( F \)は、
中心からの距離が変化せずに円運動を続けるためには、遠心力と釣り合うように中心に向かって力がかかっていなければならない。
そのため円運動を続ける条件は、「円の中心に向かって大きさ\( mr\omega^{2} \ \bigl( = m\frac{v^{2}}{r}\bigr) \)の力がかかっていること」である。
高校物理の家庭教師

最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!