どうも、かきのたねです。
今回は特殊相対性理論のローレンツ収縮について話していきます。
止まっている人が動いている人を見ると、縮んで見えてしまうことがわかっています。そしてその人が早ければ早いほど、より縮んでいるのです。
とても不思議ですよね。
一見信じられないこのローレンツ収縮という現象を、時間の遅れを使って説明していきます!
復習 〜時間の遅れ〜


速さ\( v \)で走っている人は止まっている人と比べて、体感時間・時計の針が進む時間・ありとあらゆる時間が\( \sqrt{1-(\frac{v}{c})^{2}} (\leq 1) \)倍ゆっくり進んでいる。
距離を測ろう
ところであなたはどのように距離を測っているだろうか?
例えば身長、本の端から端までの距離、電車の長さ…
最もよい測り方は、
「測りたい物体の端から光を発し、もう片方の端で反射した光が戻ってくるまでに何秒かかるか」
を測るのである。
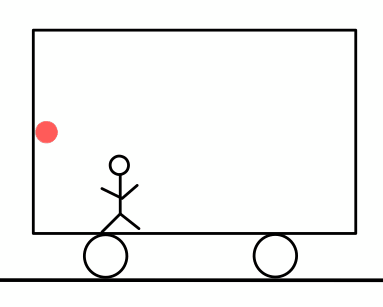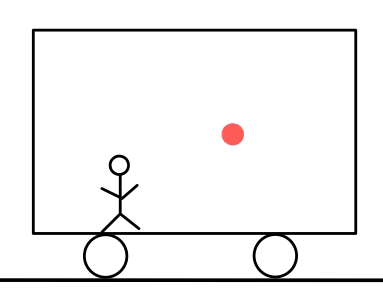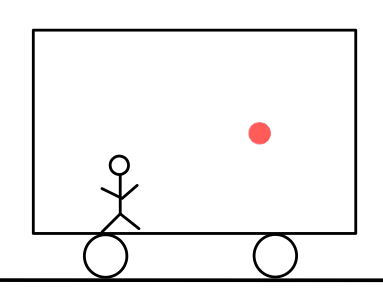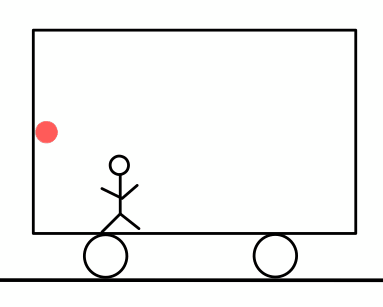
何秒(\( t \)秒)かかったかはセシウム原子時計を使い、光速\( c \)はおよそ\( 3 \times 10^{8} m/s \)である。ここから次のようにして距離\( L \)を測ることができる。
長さは光が何秒間進んだのかで測るのだ。
どんな物でもこのようにして測ることができればいいのだがそうもいかない。そのため日常生活では予め長さを測っておいたもの(定規)と比べて長さを測っている。
この記事では本来の測り方に則って長さを測る。
ローレンツ収縮 〜動くと縮む!?〜
速さ\( v \)でまっすぐに動いている電車の長さを測ってみよう。
外から止まって電車を見ている人が測る長さ\( L_{A} \)と電車の中にいる人が測る長さ\( L_{B} \)を比べてみると、とても面白い結果が得られる。
見る人によって長さが違ってしまうのだ。
これを確かめてみよう。
電車の外で静止したAさんが測った箱の長さ\( L_{A} \)
電車の外でAさんが、静止しながら電車の長さ\( L_{A} \)を測ったとしよう。
電車の後方から光を発し、前方で反射した光が再び後方に戻ってくるまでの時間\( t_{A} \)を測れば長さがわかる。
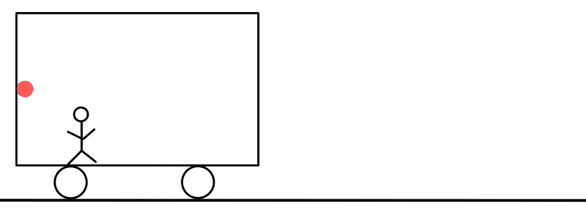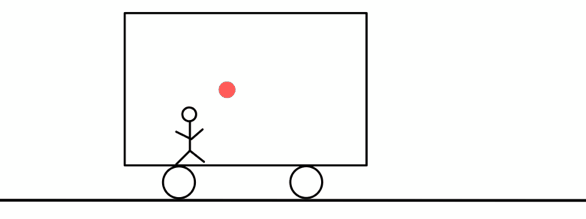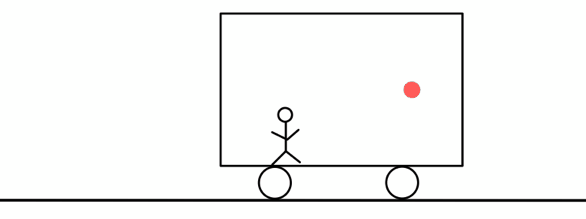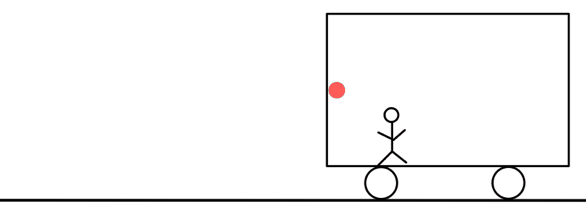

光が速さ\( c \)で前方に進んでいるときは、電車は速さ\( v \)で逃げていくので、かかる時間は\( \frac{L_{A}}{c-v} \)秒だ。
そして反射後は光の進む向きとは逆向きに電車は走っているので、かかる時間は\( \frac{L_{A}}{c+v} \)となる。
つまり長さ\( L_{A} \)の電車の長さを測ると、光の進む時間\( t_{A} \)はこのようになる。
箱の中にいるBさんが測った箱の長さ\( L_{B} \)
次に電車の中にいるBさんが、電車の長さ\( L_{B} \)を測ったとしよう。
日常生活に合わせて考えれば\( L_{A} = L_{B} \)だが、実はそうではない。確かめてみよう。
先ほどと同じように、電車の後方から光を発し、前方で反射した光が再び後方に戻ってくるまでの時間\( t_{B} \)を測る。



電車の中から見ると電車は動いていないので、光が前方に進むときも戻ってくるときも同じだけ時間がかかる。
そのため合計時間\( t_{B} \)は次のようになる。
2人が測った箱の長さ\( L_{A} \)と\( L_{B} \)の違い
先ほどの結果をまとめてみよう。
- 電車の外で静止した観測者Aから見た、光が戻ってくるまでの時間
- 電車内にいる観測者Bから見た、光が戻ってくるまでの時間
時間の遅れ\( t_{B} = \sqrt{1- \Bigl(\frac{v}{c} \Bigr)^{2}} t_{A} \)を考慮すると、\( L_{A} \)と\( L_{B} \)の関係がわかる。
なんと、\( L_{A} = L_{B} \)ではない!
電車の外で静止した観測者Aには、電車内でBが見る長さの\( \sqrt{1- \Bigl(\frac{v}{c} \Bigr)^{2}} \)倍電車が短くなったように見えるのだ。
動いているものが縮んで見える現象はローレンツ収縮という名前がついていて、どんなものでも速度の方向に\( \sqrt{1- \Bigl(\frac{v}{c} \Bigr)^{2}} \)倍縮んで見えてしまう。
動いている人の時計がゆっくり進むように見えて、そのせいで止まっている人には動いている物体が短く見えてしまうんだ。
相対性理論を勉強するときは、「時間は絶対的なものだ」という考えを出来るだけなくせるようにしよう!
高校物理の家庭教師


最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!








taとtbの関係式で、taとtbの位地が逆になっていると思いますが?!
ご指摘いただきありがとうございます。
こちらで確認したところ確かにtaとtbを書き間違っておりましたので、先ほど修正いたしました。
これからもご活躍されるよう祈っております。