どうも、かきのたねです。
平行平板コンデンサーの公式\( C=\frac{\epsilon _{0}S}{d} \)はよく使う公式ですが、この公式の導出方法は覚えていない人が多いと思います。今回はなぜ電気容量が\( C=\frac{\epsilon _{0}S}{d} \)となるのかを解説します。
電気容量とは
コンデンサーは電気を蓄えておくことができるのは知っていることだろう。電気を貯めるときにはコンデンサーに電圧をかけるのだが、貯まる電気量は電圧に比例することが知られている。
この比例定数\( C \)を電気容量という。
電気量\( Q \)が蓄えられたコンデンサーにはどれだけの電圧\( V \)がかかっているかを求め、電気容量\( C \)の表式を求める。
帯電した1枚の平極板が作る電場
電気力線
電場の様子(向きと大きさ)を表す量に電気力線というものがある。
電気力線は次のように決められている。
- 電気力線は電場と平行
- 電気力線の密度は電場の強弱を表す
- 電気量\( Q \)の電荷から出てくる電気力線の本数\( N \)は
\( \epsilon \)は誘電率で、真空の誘電率は\( \epsilon_{0} \)と書くことが多い。
誘電体の誘電率\( \epsilon \)は、\( \epsilon_{r} \)に真空中の誘電率\( \epsilon_{0} \)を掛け算したものである。
誘電体が電場の中にある(真空中)と片側が正に帯電し、もう片側が負に帯電する(分極)のは知っているかな?
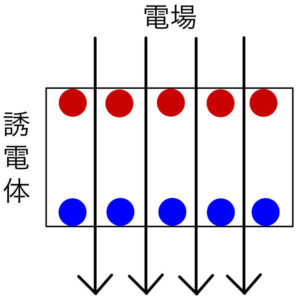

分極すると誘電体には、加えられた電場を打ち消そうとする電場が生じる。
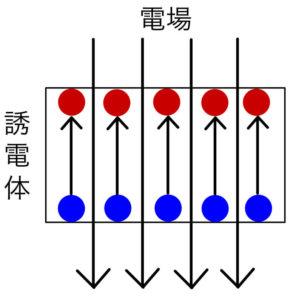

そうすると誘電体の中の電場は弱まる。電場がどれだけ弱まってしまうのかを表すのが\( \epsilon_{r} \)だ。
電気力線で見てみれば、本数\( N \)が誘電体内で減ったと言える。真空中での電気力線の本数を\( N_{0} \)とすると、次の式で書ける。
\( N_{0} = \frac{Q}{\epsilon_{0}} \)を使うと、このようになる。
一般に誘電体の誘電率\( \epsilon \)には\( N = \frac{Q}{\epsilon} \)の関係があったことを思い出すと、
だとわかる。
誘電体の誘電率\( \epsilon \)は真空中の誘電率\( \epsilon_{0} \)の\( \epsilon_{r} \)倍だから、この\( \epsilon_{r} \)のことを比誘電率と言う。
電気力線の本数と電場の関係
電気力線の密度は電場の大きさを表すのであった。
面積\( S \)のある断面から垂直に\( N \)本の電気力線が飛び出しているとき、その断面での電場\( E \)は次のように書く。
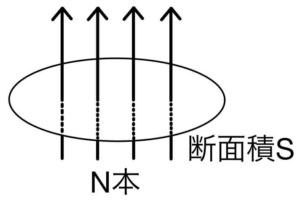

帯電した平極板が作る電場
断面積\( S \)の平極板に電気量\( Q \)でけ蓄えられているとき、この平極板からは\( \frac{Q}{\epsilon} \)本の電気力線が出ている。
平極板は大きく端での電場の漏れだしを無視できるとすると、極板の上下に半分ずつの電気力線が出ていることになる。
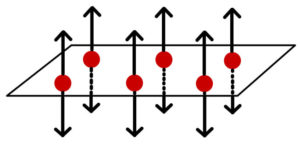

そのため上側も下側も電場の大きさ\( E \)は同じで、次のようになる。
これで1枚の帯電した平極板のつくる電場がわかった。
電気容量の求め方
2枚の極板間の電位差
次は正に帯電した極板と負に帯電した極板とを平行に並べたときに、極板間の電場がどうなるか見てみよう。
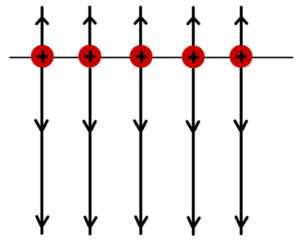

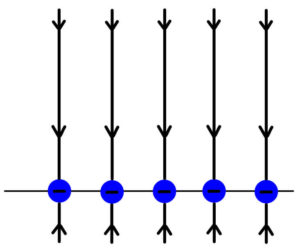

これらの極板を平行に配置すると、次のようになる。
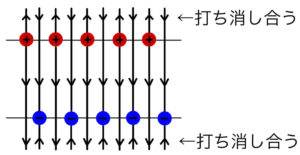

2枚の極板ではそれぞれ電場の向きが逆になるので、重ね合わせると打ち消しあう。
また極板間の電場はどちらも大きさ\( \frac{Q}{2\epsilon S} \)で同じ向きなので、重ね合わせると次のようになる。
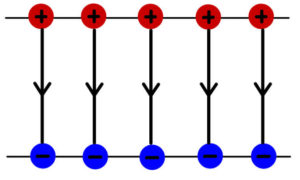

極板間の距離が\( d \)の時、電位差\( V \)は次のように求められる。
電気容量を求める
\( Q \)と\( V \)の関係は
なので、電気容量\( C \)を求めることができる。
極板間が真空であったとき、\( C = \frac{\epsilon_{0} S}{d} \)となる。
まとめ
- 帯電した1枚の平極板からは、大きさ\( \frac{Q}{2\epsilon_{0} S} \)の電場が生じる
- 正負に帯電した2枚の極板間の電場は\( E = \frac{Q}{\epsilon_{0} S} \)
- 極板間の電位差は\( V = Ed = \frac{d}{\epsilon_{0} S}Q \)
- 電気容量は\( C = \frac{\epsilon_{0} S}{d} \)
具体例として次のようなコンデンサーで電気容量を求めてみよう!


高校物理の家庭教師


最後まで読んでくださり、ありがとうございます(`・∀・´)
Twitterで更新情報などをツイートするので、少しでもこの記事が面白いと思っていただけたら是非フォローお願いします!
この分野の説明をして欲しいといったリクエストも随時募集しております。お問い合わせやTwitterなどからご連絡下さい!